Proportionnalité
I-Activité
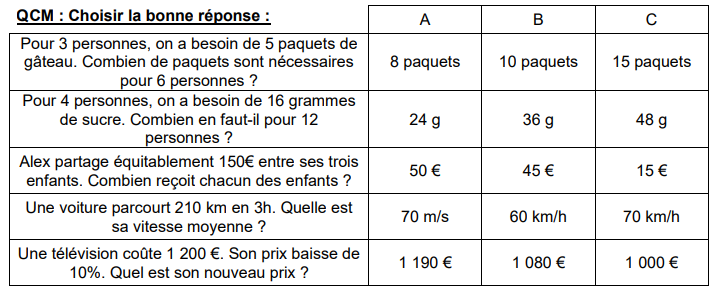
II. Définition de la proportionnalité
Deux grandeurs sont proportionnelles si l’on peut calculer la mesure de l’une en multipliant la mesure de l’autre par un coefficient toujours le même appelé le coefficient de proportionnalité.
Exemple 1
« Papa prend 40 Litres de carburant et paie 62,40 €. La semaine suivante, il prend 24 Litres de carburant. Combien paie-t-il ? »
Les deux grandeurs sont : le nombre de litres de carburant et le prix du carburant.
Pour calculer le prix d’un plein, on multiplie le nombre de litres de carburant par le prix d’un litre.
C’est une situation de proportionnalité et le coefficient de proportionnalité est le prix d’un litre.
On calcule le prix d’un litre :
62,50 ÷ 40 = 1,56
Donc un litre coûte 1,56 €.
24 × 1,56 = 37,44
Pour 24 litres, il paie 37,44 €.
Exemple 2
« Pierre a 15 ans et mesure 1,65 mètre. Combien mesura-t-il à 30 ans. »
Les deux grandeurs sont : l’âge de Pierre en année et sa taille en mètre.
Ces deux grandeurs ne sont pas proportionnelles donc cette situation n’est pas une situation de proportionnalité.
On ne peut donc pas savoir la taille de Pierre à 30 ans.
III. Tableau de proportionnalité
1- Comment reconnaître un tableau de proportionnalité ?
Le tableau ci-dessous est-il un tableau de proportionnalité ?
Pour calculer le périmètre d’un carré, on doit multiplier le côté par 4. C’est une situation de proportionnalité.
Le tableau correspondant est un tableau de proportionnalité.
On remarque que le quotient de la valeur d’arrivée par la valeur de départ est toujours un nombre constant :
En effet 12/3 = 20/5 = 32/8 = 60/15 = 4, appelle ce nombre le coefficient de proportionnalité du tableau.
Le tableau ci-dessous est-il un tableau de proportionnalité ?
Par contre, pour le calcul d’aire, ce n’est pas une situation de proportionnalité. En effet, pour calculer l’aire d’un carré, on multiplie le côté par lui-même.
On remarque que le quotient de la valeur d’arrivée par la valeur de départ n’est pas un nombre constant :
En effet 9/3 ≠ 25/5 ≠ 64/8 ≠ 225/15, donc le tableau correspondant n’est un tableau de proportionnalité.
2- Comment compléter un tableau de proportionnalité ?
Pour remplir un tableau de proportionnalité, on peut :
- Ajouter deux colonnes pour en obtenir une troisième ;
- Multiplier ou diviser une colonne pour en obtenir une deuxième ;
- Calculer le coefficient de proportionnalité ;
Exemple 3
Voici un tableau qui nous donne la consommation d’une voiture en fonction de la distance parcourue :
Pour calculer pour 100 km, il suffit de multiplier la première colonne par 2.
En effet 50 × 2 = 100, du coup 2,4 × 2 = 4,8.
Ensuite, comme 50 + 100 = 150, en ajoutant les deux premières colonnes, on
obtient la troisième : 2,4 + 4,8 = 7,2.
On peut aussi calculer le coefficient de proportionnalité.
Pour cela, il suffit de calculer la consommation pour 1 km.
2,4 ÷ 50 = 0,048
200 × 0,048 = 9,6.
Pour la dernière colonne, on peut aussi utiliser la propriété suivante appelée la quatrième proportionnelle.
IV. Quatrième proportionnelle
1- Définition
La quatrième proportionnelle est le quatrième nombre à mettre dans un tableau de proportionnalité à 4 valeurs dont 3 cases sont déjà remplies.
Ce quatrième nombre s’obtient en faisant le produit des nombres situés sur une même diagonale et en divisant par le troisième nombre.
Cette technique est parfois appelée « règle de trois » ou « produit en croix ».
Reprenons le tableau précédent, on souhaite trouver le nombre a, c’est notre quatrième proportionnelle.
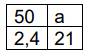
comme le tableau précédent est un tableau de proportionnalité, on peut effectuer le produit 50 × 21 = 2,4 × a
On an donc a = (50 × 21) ÷ 2,4 = 437,5
V. Représentation graphique
1- Exemple
Le tableau ci-dessous représente le prix d’une corde pour alpiniste en fonction de sa longueur.
Ce tableau est un tableau de proportionnalité.
La situation est proportionnelle.
On veut représenter cette situation sur un graphique.
Pour cela on se munit d’un repère avec sur l’axe des abscisses la longueur en mètres de la corde et sur l’axe des ordonnées le prix en euros.
On place les points (10 ; 15) ; (20 ; 30) ; (30 ; 45) ; (50 ; 75) et (100 ; 150).
On relie les points.
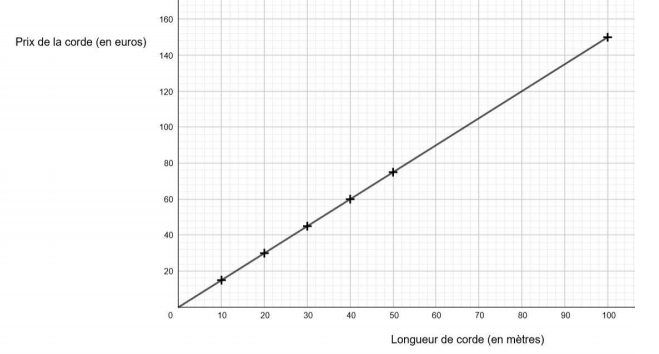
2- Propriété
Une situation de proportionnalité est représentée graphiquement par des points alignés sur une droite passant par l’origine du repère.
METHODE :
On peut se servir de cette propriété pour dire si une situation est proportionnelle ou non. On observe la représentation graphique de la situation et si on observe une droite qui passe par l’origine, alors on peut conclure que la situation est proportionnelle.
3- Exemple
Situation 1
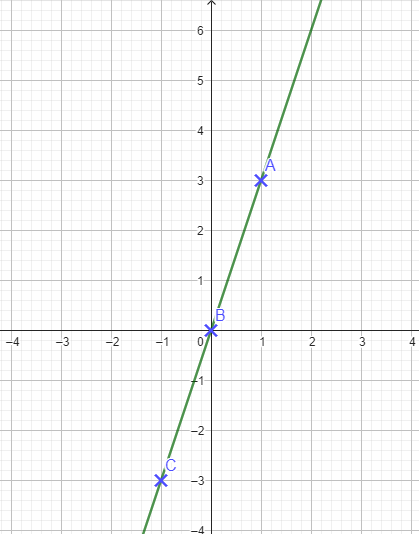
Situation 2
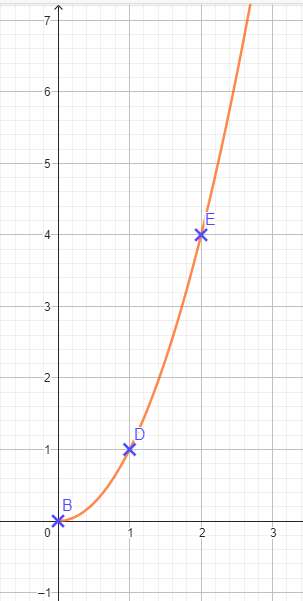
Situation 3
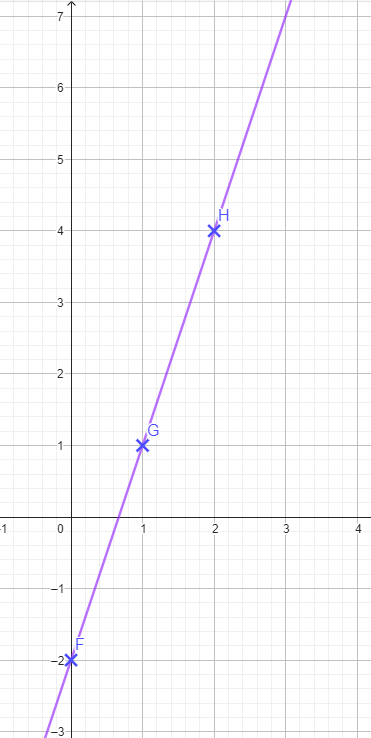
Seule la situation 1 est une situation de proportionnalité.
La situation 2 n’est pas représentée par une droite.
La situation 3 est représentée par une droite mais elle ne passe pas par l’origine du repère (le point (0 ; 0)).