Arithmétique (Partie 1)

I. Vocabulaire et définitions

a) Qu’est-ce qu’une division euclidienne ?

Euclide 300 avant J-C Source (https://fr.wikipedia.org/wiki/Euclide)

Définition : Effectuer la division euclidienne de a par b, c’est trouver le quotient q et le reste r tels que :

a = b x q + r et 0 ≤ r < b

Effectuer la division euclidienne de 349 par 6 signifie :

Dans 349 combien y-a-t-il de 6 ?

Dans 349, il y a 49 fois 7 et il reste 6 Soit 349 = 49×7 + 6

Avec la calculatrice, on peut effectuer la division euclidienne de 349 par 7

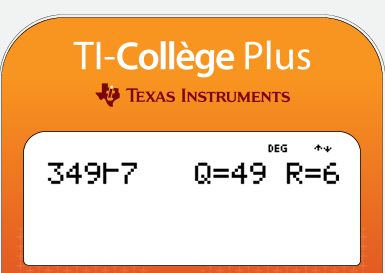
Exercice d’application

• Effectue la division euclidienne de 183 par 12.
• 278 = 6 × 45 + 8 : quelle(s) division(s) euclidienne(s) cette égalité
  représente-t-elle ?

b) Comment savoir si un nombre est diviseur d’un autre nombre ?

Définition : Un nombre a est divisible par un nombre b lorsque le reste de la division euclidienne de a par b est nul, c’est à dire lorsque le quotient de a par b est un nombre entier.
On dit alors que b est un diviseur de a et que a est un multiple de b
Remarques :
● 1 est un diviseur de tout entier
● Chaque entier est divisible par lui-même.
Exemple :
● 18 est divisible par 6 car 18 = 6 × 3 + 0
On dit que 6 et 3 sont des diviseurs de 18 et que 18 est un multiple de 6 et de 3.

c) Connaître les critères de divisibilité

Un critère de divisibilité est un moyen de savoir si un nombre est divisible par un autre nombre sans avoir à poser la division.
Un nombre entier est divisible :
❏ par 2, si son chiffre des unités est pair
❏ par 5, si son chiffre des unités est 0 ou 5
❏ par 10, si son chiffre des unités est 0
❏ par 3, si la somme de ses chiffres est divisible par 3
❏ par 9, si la somme de ses chiffres est divisible par 9 ❏ par 4, si ses deux derniers chiffres forment un multiple de 4.​ ​ 

Exemples :

81 630 est…
❏ divisible par 2 parce qu’il est pair ;
❏ divisible par 5 parce que son chiffre est unités est 0 ;
❏ divisible par 3 parce que 8 + 1 + 6 + 3 + 0 = 18 et 18 est divisible par 3 (3 × 6 =18).

❏ divisible par 9 parce que 8 + 1 + 6 + 3 + 0 = 18 et 18 est divisible par 9 (9 × 2 =18).

Exercice d’application

• 1 290 est-il divisible par :
  • 2 ?
  • 3 ?
  • 5 ?
  • 9 ?

d) Comment savoir si un nombre est diviseur d’un autre nombre ?

Définition : Un nombre a est divisible par un nombre b lorsque le reste de la division euclidienne de a par b est nul, c’est à dire lorsque le quotient de a par b est un nombre entier.
On dit alors que b est un diviseur de a et que a est un multiple de b
Remarques :
● 1 est un diviseur de tout entier
● Chaque entier est divisible par lui-même.
Exemple :
● 18 est divisible par 6 car 18 = 6 × 3 + 0
On dit que 6 et 3 sont des diviseurs de 18 et que 18 est un multiple de 6 et de 3.

Activité

Quel est  le chemin qui vous permet d’atteindre la sortie en passant uniquement par les multiple de 11 ?

e) Comment trouver tous les diviseurs d’un entier naturel ?

Propriété : Pour trouver tous les diviseurs d’un nombre entier 𝑛, on teste la divisibilité de 𝑛 par tous les nombres entiers inférieurs ou égaux à √𝑛.

Exemple : Pour trouver tous les diviseurs de 100, on teste la divisibilité avec tous les entiers inférieurs ou égaux à 10.

Méthode commentée en vidéo

Activité : « LE PROBLÈME DU CENTURION »​

Le centurion ordonne à ses légionnaires : « Rangez-vous par 4 ! ».

Les soldats s’exécutent, mais le dernier rang est
incomplet : il ne compte que 3 soldats.

« Mettez-vous par 5 ! », hurle alors le centurion ; mais au dernier rang,
incomplet, on compte de nouveau 3 soldats.

« Eh bien, rangez-vous par 7 ! ». Encore une fois, le dernier rang reste
incomplet : on y compte toujours 3 soldats.

Pour revoir le vocabulaire et les critères de divisibilité

Pages : 1 2 3 4 5 6 7