Translation
Activité d’introduction

Transformer une figure par translation

1) Définition
Transformer une figure par translation revient à la faire glisser d’une longueur donnée, le long d’une droite donnée et dans un sens donné.
Remarque : La longueur, la direction et le sens peuvent être donnés.
2) Tracé le translaté d’un point à l’aide du quadrillage
Construire l’image du point B par la translation qui transforme A en A’
Pour construire l’image du point B, on reproduit « la flèche rouge » en plaçant son origine en B. On peut s’aider du quadrillage.
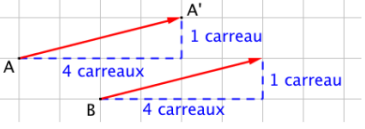
On obtient le pont B’ tel que les deux flèches rouges aient la même direction, le même sens et la même longueur.
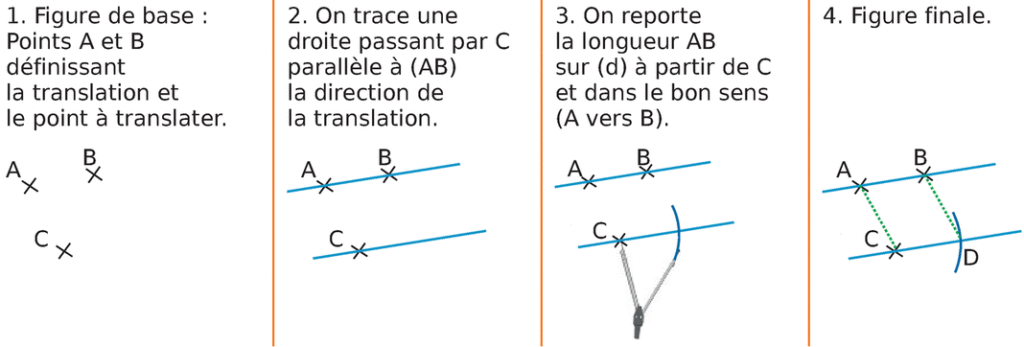
2) Tracé le translaté d’un point sans le quadrillage
Propriété
Si la translation qui transforme A en A’ transforme aussi M en N, alors AA’NM est un parallélogramme éventuellement aplati si les points sont alignés.
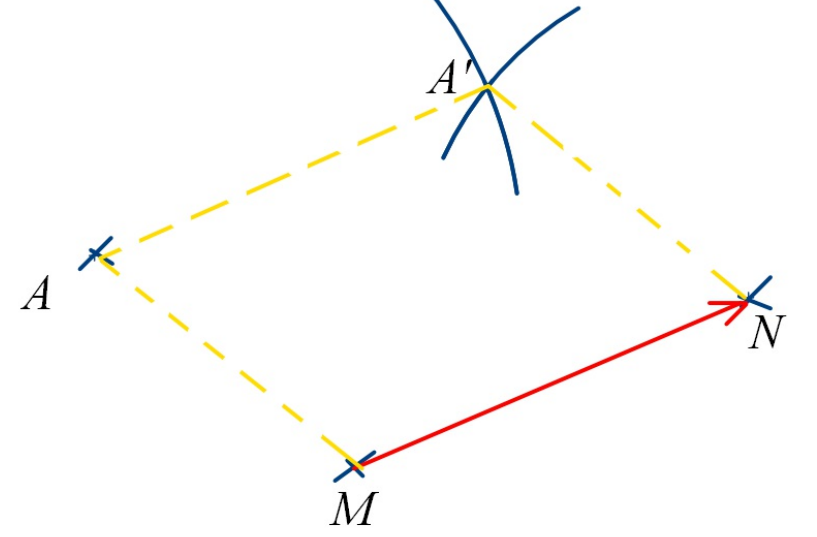
Méthode
La translation conserve l’alignement, les longueurs, le parallélisme et les angles.
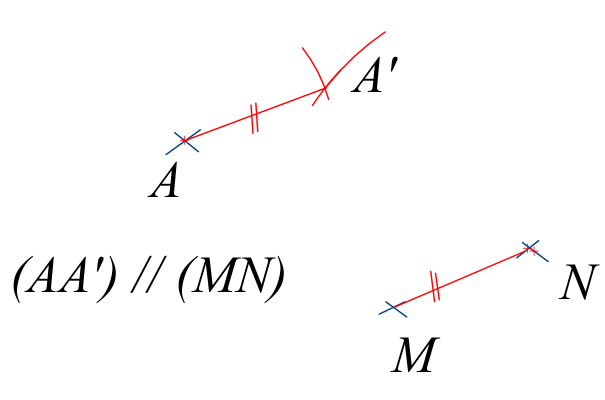
A’ est le translaté (l’image) du point A par la translation qui transforme M en N.
On obtient le parallélogramme AA’NM
3) Tracé le translaté d’une figure
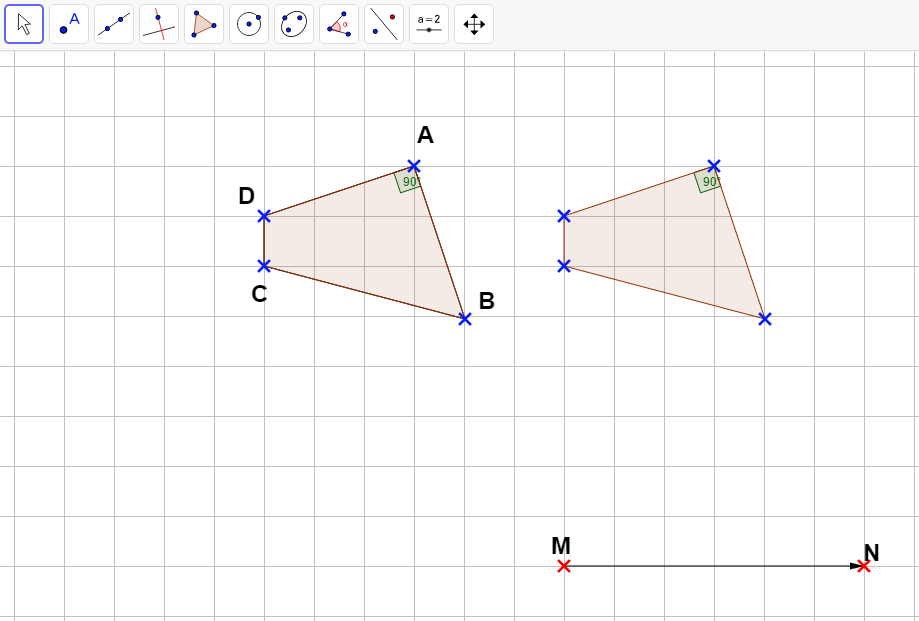
AB’C » est le translaté (l’image) du triangle ABC par la translation qui transforme M en N.
On procède point par point, on place l’image du point A, celle du point B et enfin celle du point C.
On relie ensuite les trois points obtenus.
Le translaté d’une figure est une figure qui lui est superposable par glissement.
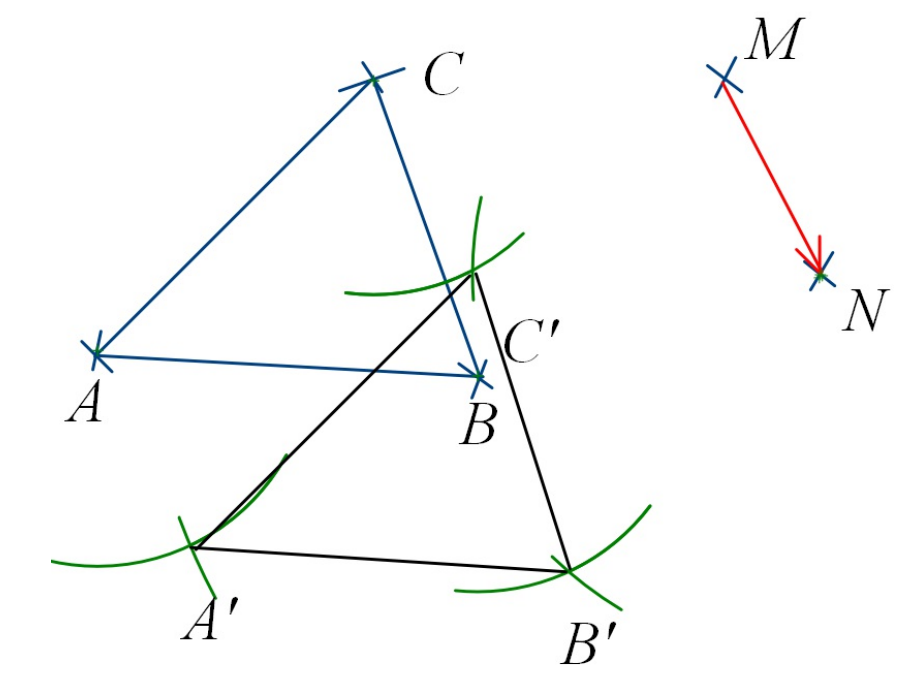
Illustration de la translation avec GeoGebra