Transformer une figure par symétrie ou translation ou rotation

Activité d’introduction

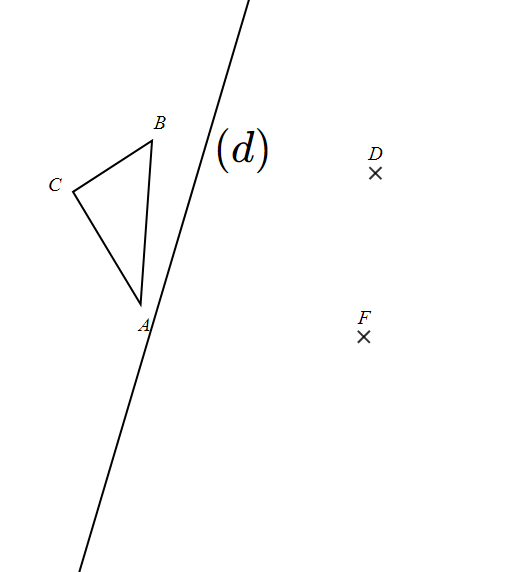
Construire
A₁B₁C₁​ le triangle symétrique de ABC par rapport à la droite (d).
A₂B₂C₂ le triangle symétrique de A₁B₁C₁ par rapport au point D.
A₃B₃C₃ le triangle translaté de A₂B₂C₂ par la translation qui transforme D en F.
A₄B₄C₄ le triangle obtenu par la rotation de A₃B₃C₃ de centre F et d’angle 88° dans le sens des aiguilles d’une montre.

Rappel de cours

1-La symétrie axiale

Deux figures sont symétriques par rapport à une droite (d), si elles sont parfaitement superposables selon cet axe (d).

La droite (d) est alors la médiatrice de tous les segments formés par les points et leurs symétriques respectifs.

Méthode

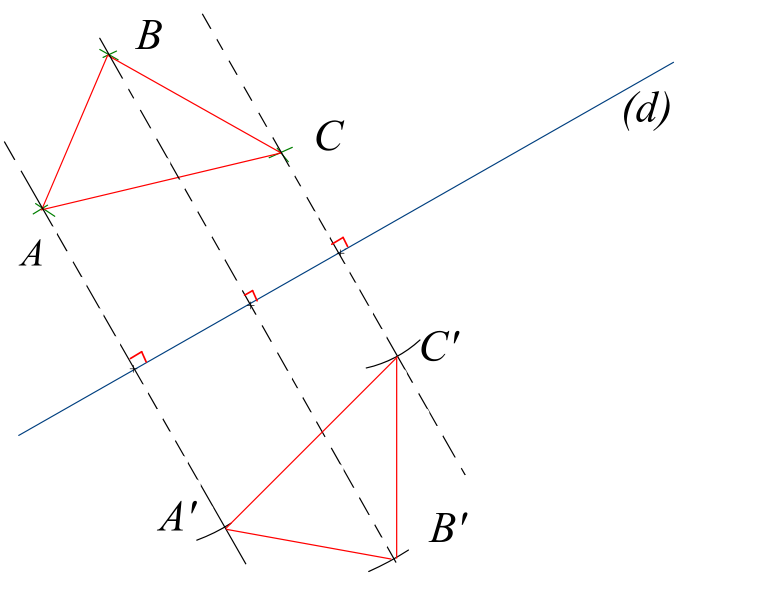
Illustration de la symétrie axiale avec GeoGebra

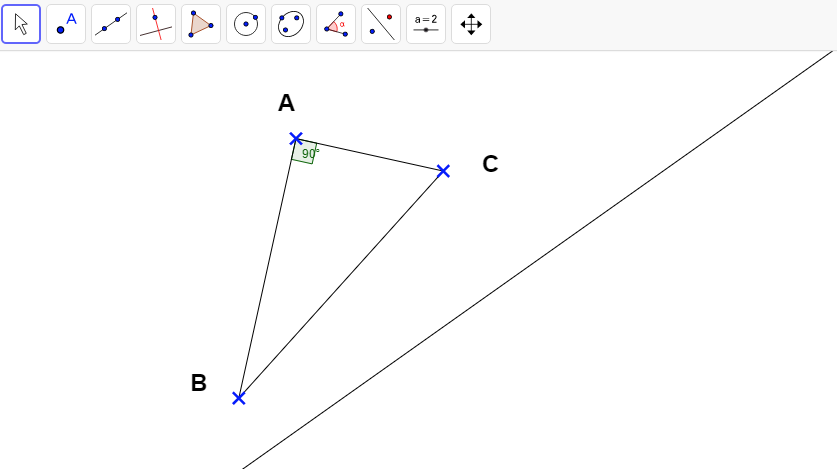
Propriété

La symétrie axiale conserve l’alignement, les longueurs, le parallélisme et les angles.

2-La symétrie centrale

Transformer une figure par symétrie centrale revient à lui faire faire un demi-tour autour d’un point.

Deux points A et A’ sont symétriques par rapport au point O lorsque le point O est le milieu du segment [AA’].

Méthode

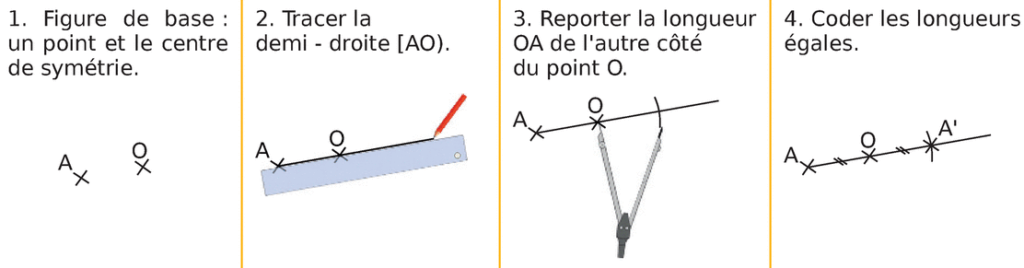
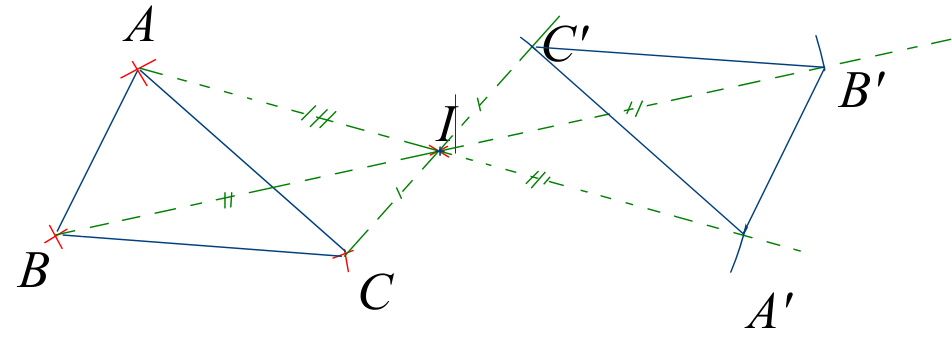
Propriété

La symétrie centrale conserve l’alignement, les longueurs, le parallélisme et les angles.

Illustration de la symétrie centrale avec GeoGebra

3-La translation

Transformer une figure par translation revient à la faire glisser d’une longueur donnée, le long d’une droite donnée et dans un sens donné.

Remarque : La longueur, la direction et le sens peuvent être donnés.

Propriété

Si la translation qui transforme A en A’ transforme aussi M en N, alors AA’NM est un parallélogramme éventuellement aplati si les points sont alignés.

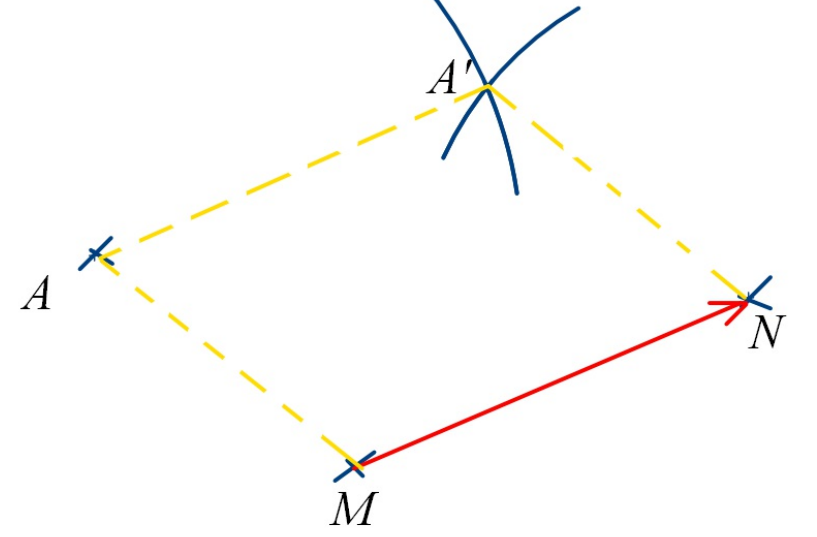
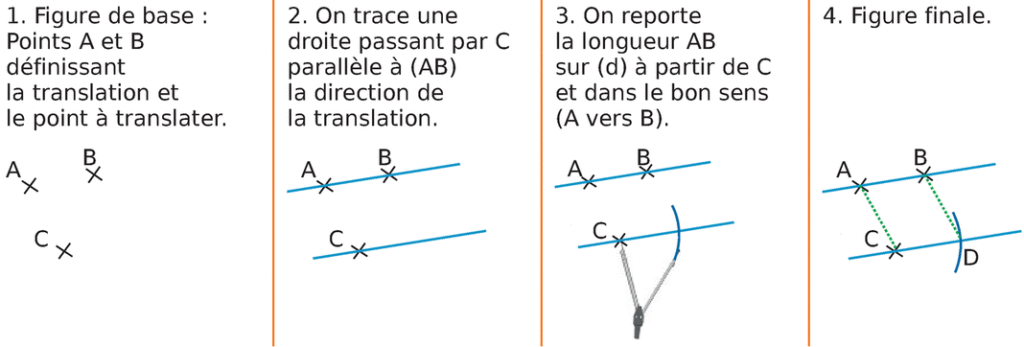
Méthode

La translation conserve l’alignement, les longueurs, le parallélisme et les angles.

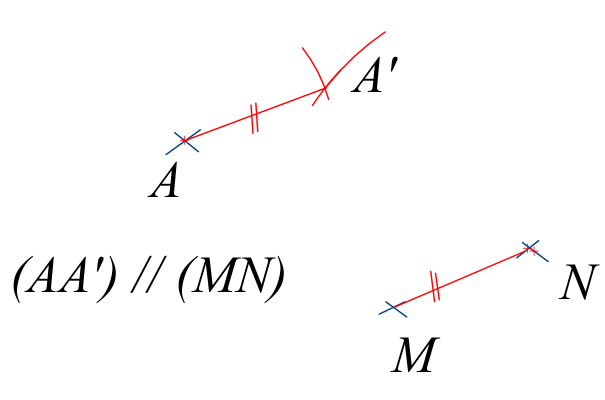
A’ est le translaté (l’image) du point A par la translation qui transforme M en N.

Remarque :

AB’C » est le translaté (l’image) du triangle ABC par la translation qui transforme M en N.

Le translaté d’une figure est une figure qui lui est superposable par glissement.

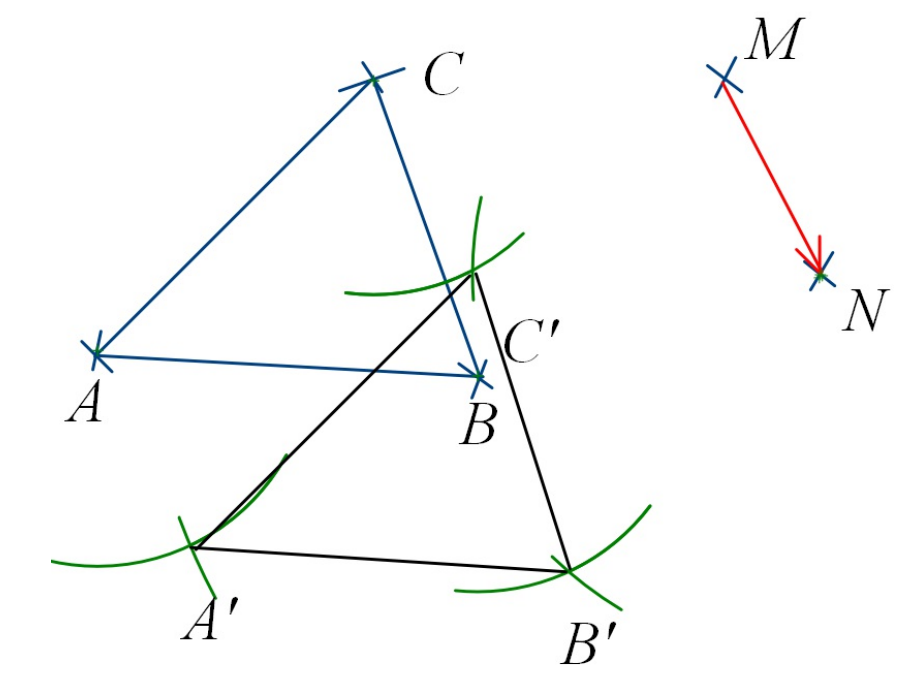
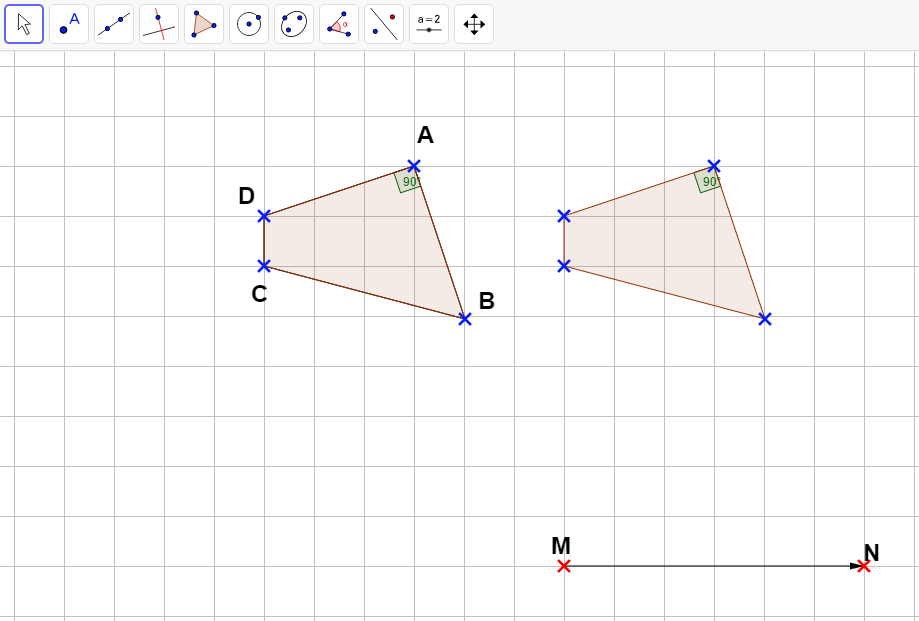
Illustration de la translation avec GeoGebra

4-La rotation

Transformer une figure par rotation revient à la faire pivoter d’un angle donné autour d’un point, son centre. Le sens inverse des aiguilles d’une montre est appelé sens direct ou le sens anti-horaire.

Illustration de la rotation avec GeoGebra

Exemple :

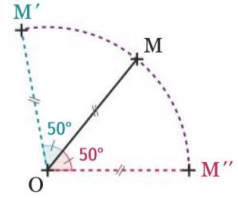
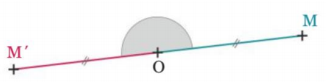
L’image d’un point M par la rotation de centre O et d’angle 50° est le point M’
Méthode

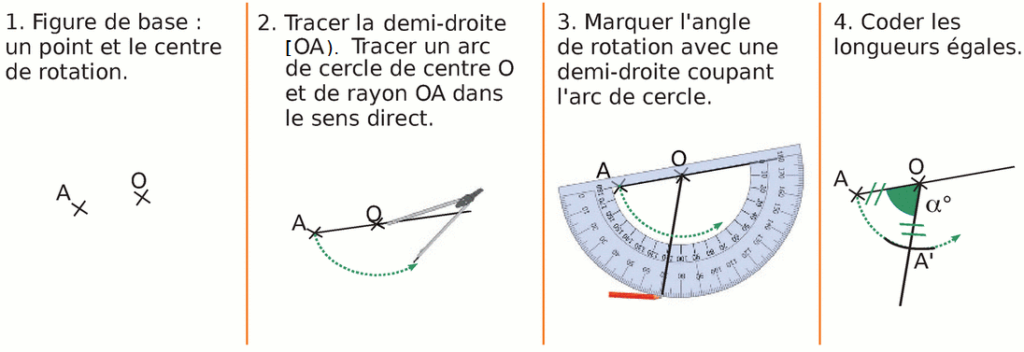
Propriété

La rotation conserve l’alignement, les longueurs, le parallélisme et les angles.

Exemples :

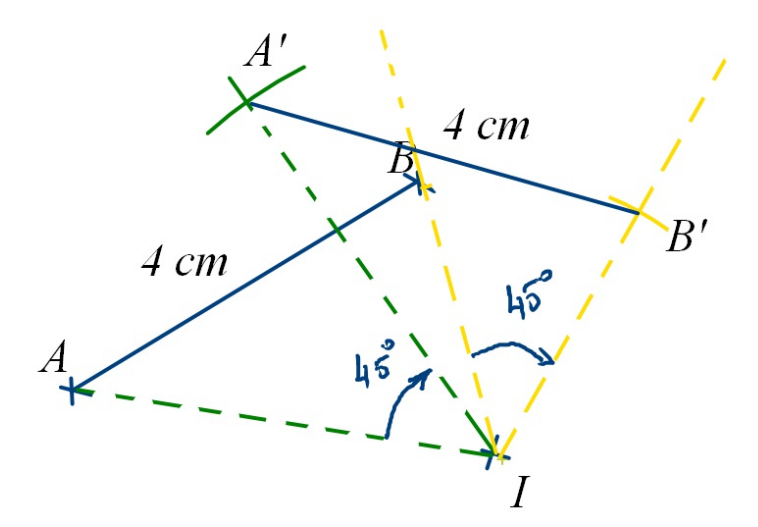
[A’B’] est l’image de [A’B’] par la rotation de centre I, d’angle 45° dans le sens horaire.

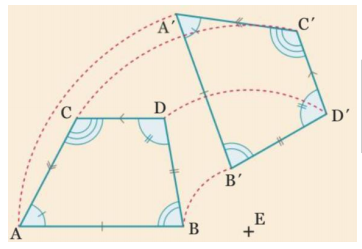
A’B’C’D’ est l’image de ABCD par la rotation de centre E, d’angle 70° dans le sens horaire.

[AB] // [CD] et [A’B’] // [C’D’]

Remarques :
1) Le centre d’une rotation est un point invariant, c’est-à-dire que son image par cette rotation est lui-même.

2) Une rotation de centre O et d’angle 180° (quel que soit le sens de rotation) est une symétrie centrale de centre O.

Exemple :
Tous les triangles de la figue ci-contre sont des triangles équilatéraux.

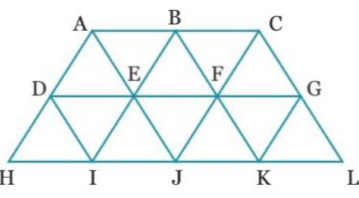
1) Quelle est l’image de F par la rotation de centre E et d’angle 60° dans le sens antihoraire ?
2) Quelle est l’image de F par la rotation de centre E et d’angle 120° dans le sens horaire ?
3) Quelle est l’image de I par la rotation de centre K et d’angle 60° dans le sens horaire ?

Pages : 1 2 3