Objectifs

Activités

Activité- 1: De la symétrie axiale vers la symétrie centrale…

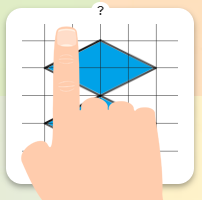
Activité- 2 : La symétrie centrale… Un demi-tour ?

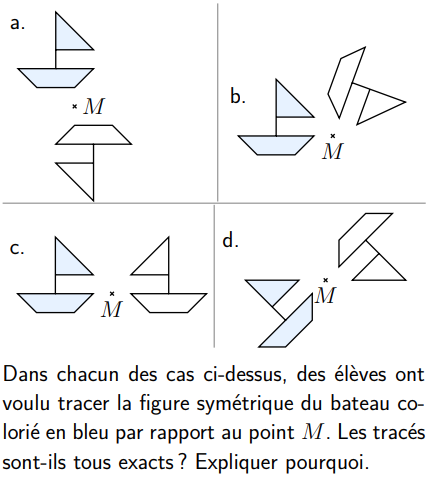
Activité- 3 : Le symétrique d’un bateau

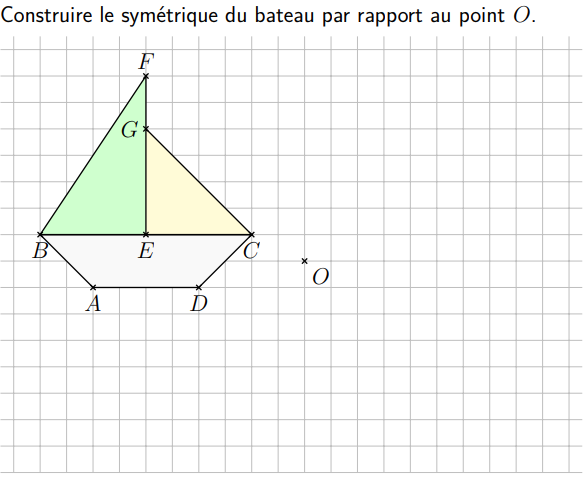
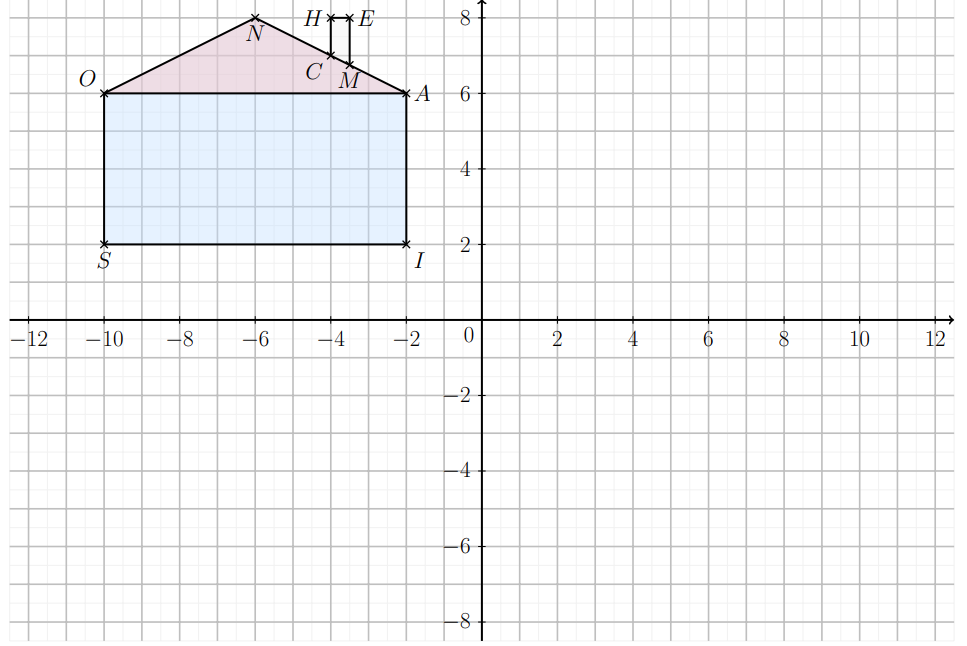
Activité- 4 : Le symétrique d’une montgolfière sans quadrillage

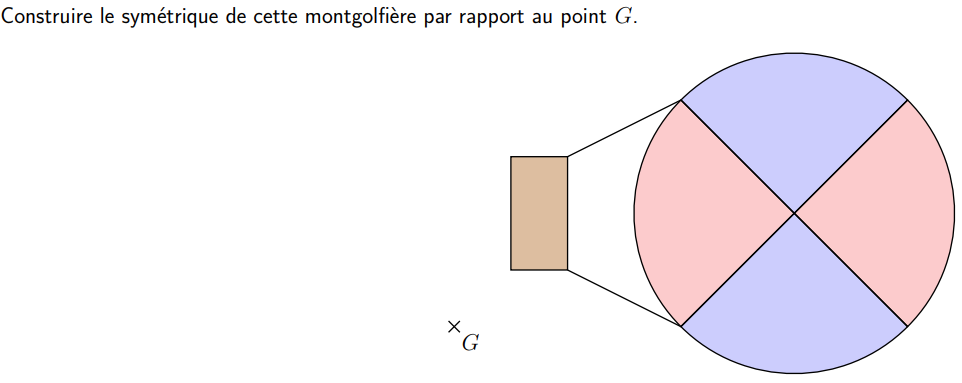
Symétrie centrale

1-Construire le symétrique d’un point

Propriété

Deux points A et A’ sont symétriques par rapport au point Olorsque le point O est le milieu du segment [AA’].

Méthode

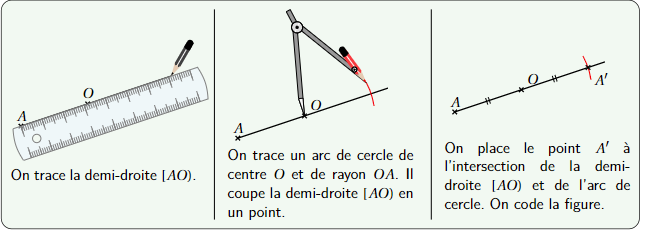
2-Construire le symétrique d’un segment

Méthode

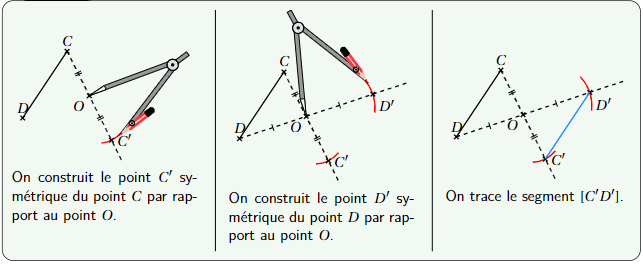
Pour tracer le symétrique d’un segment, il suffit de tracer les symétriques de ses extrémités.

 

 

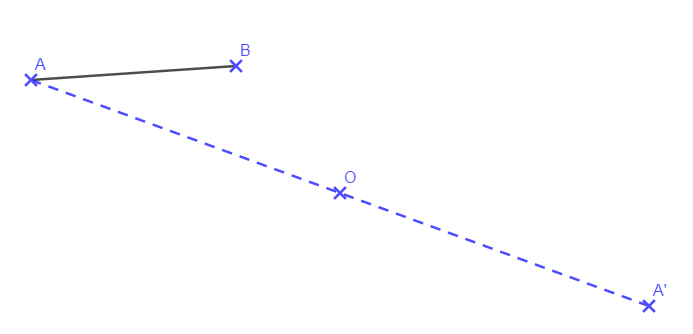
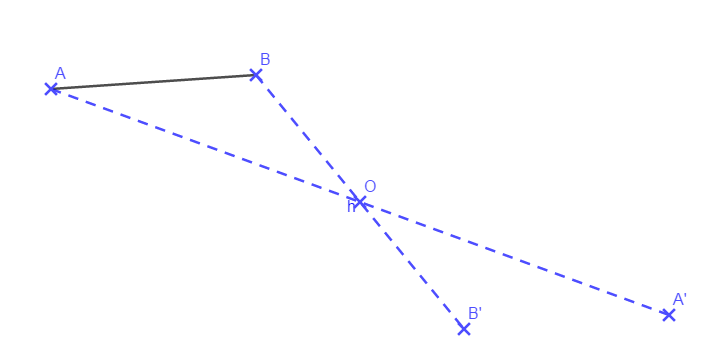
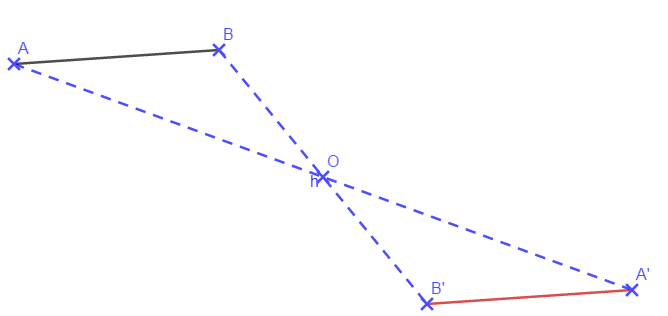
Exercice d’application

3-Construire le symétrique d’un cercle

Méthode

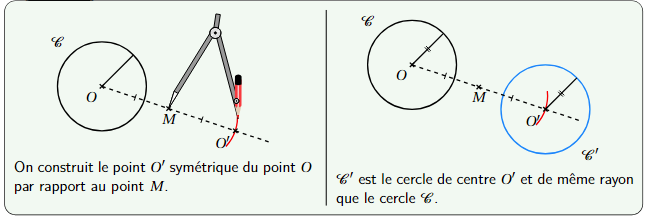
Pour tracer le symétrique d’un cercle, il suffit de tracer le symétrique de son centre.

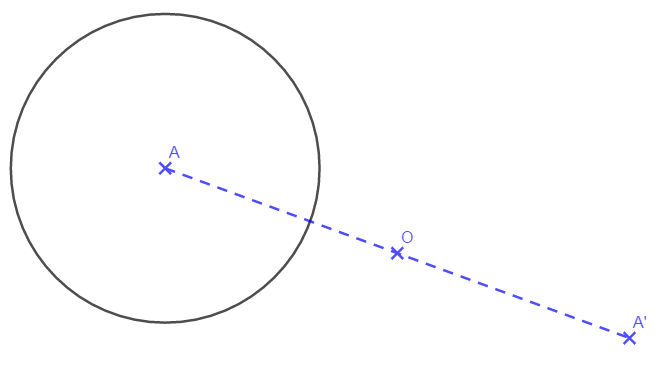
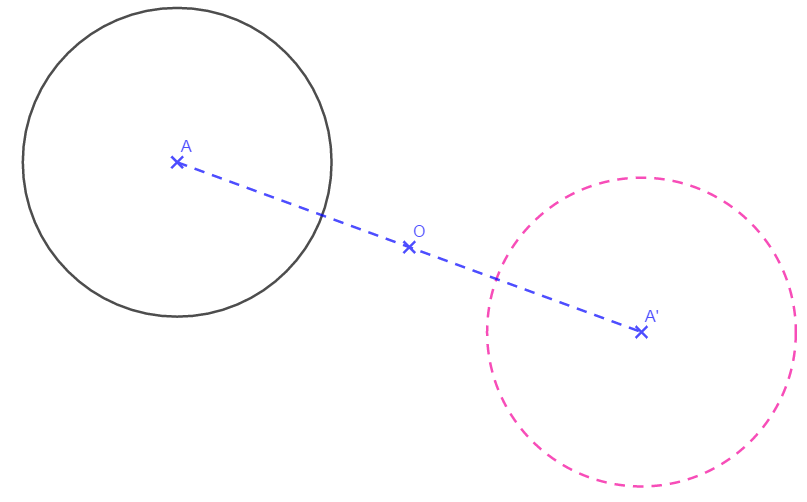
4-Construire le symétrique d’une figure

Propriété

Le symétrique d’une figure par rapport à un point s’obtient par un demi tour autour de ce point. On obtient donc une figure qui lui est identique.

La symétrie centrale conserve l’alignement, les longueurs, le parallélisme et les angles.

Méthode

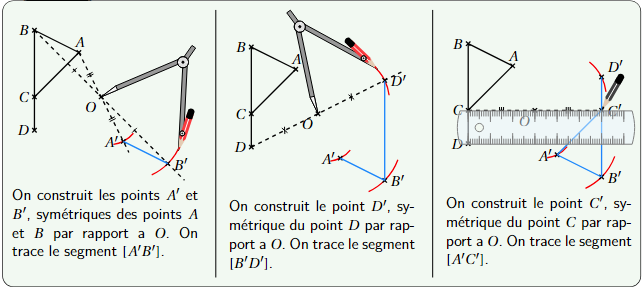
Exemple

Pour tracer le symétrique d’un triangle, il suffit de tracer les symétriques de ses sommets.

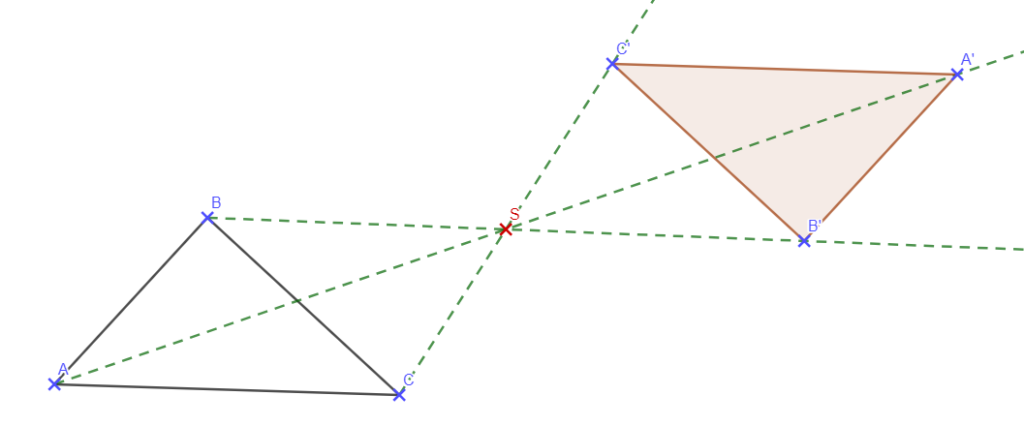
5-Centre de symétrie

Propriété

Une figure possède un centre de symétrie si son symétrique par rapport à ce centre est elle même.

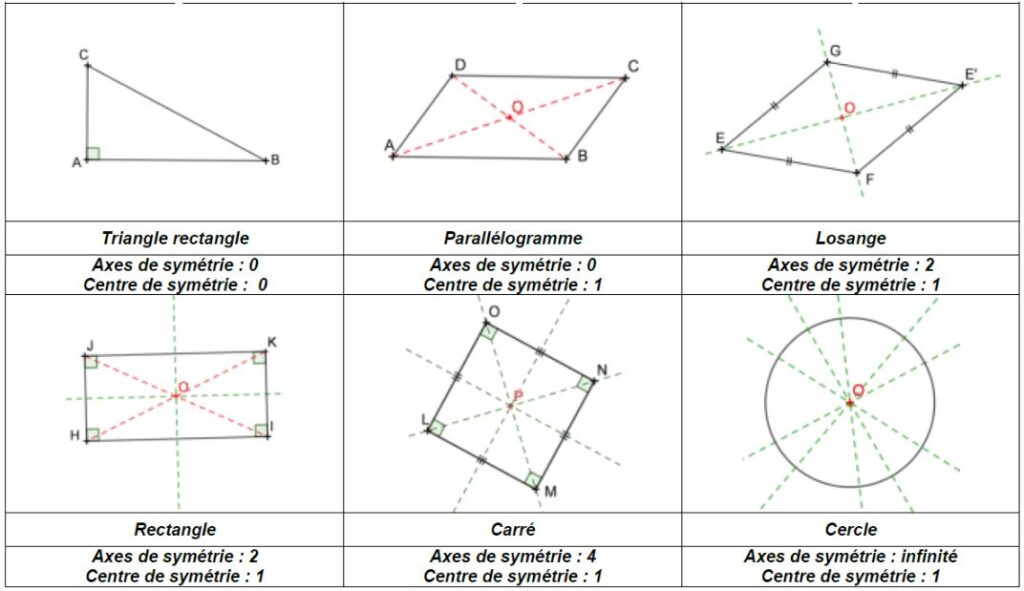
Exemples

Ces figures admettent-elles un centre de symétrie ?

Exercice sur les axes de symétrie

QCM

Construction et transformation de figures

 Tracer le symétrique d’un point par rapport à une droite

 Tracer le symétrique d’un point par rapport à un point

 Tracer le symétrique d’une figure par rapport à un point

Fiche d’exercices

Exercice 1 *

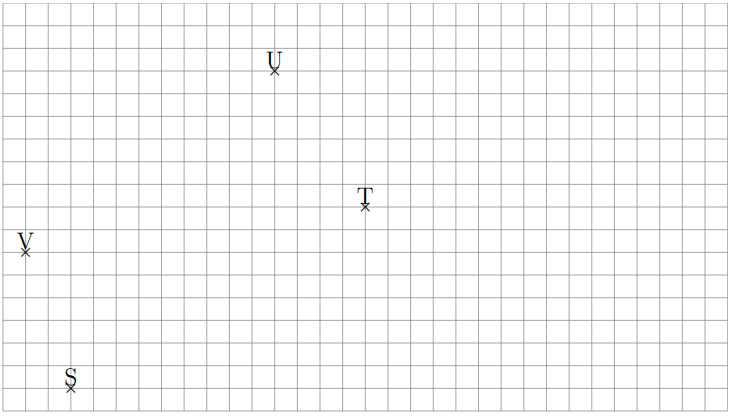
a. Construire le point U’ symétrique de U par rapport au point T.
b. Construire le point V’ symétrique de V par rapport au point T.
c. Construire le point S’ symétrique de S par rapport au point T.
d. Coder la figure.

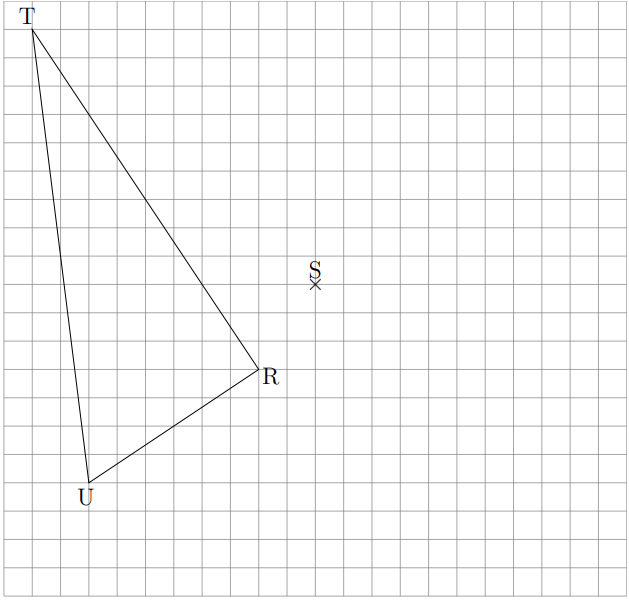
Exercice 2 **

a. Construire le triangle R’T’U’symétrique de RTU par rapport au point S.
b. Coder la figure.

Exercice 3 *

Construire les symétriques W’, T’ et C’ respectifs des points W, T et C par rapport au point X.

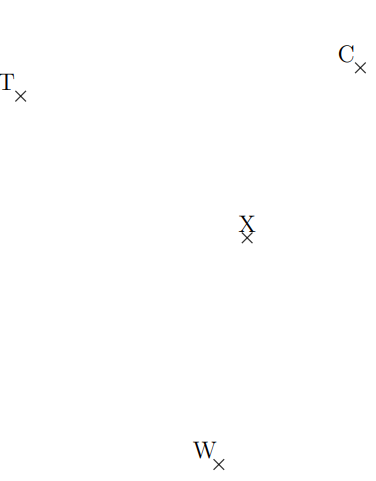
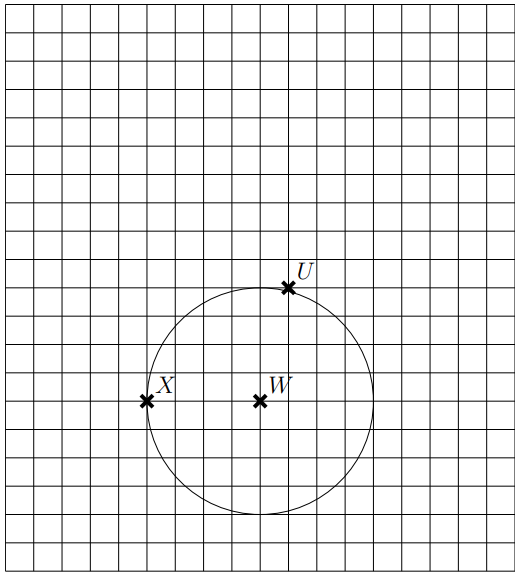
Exercice 4 *

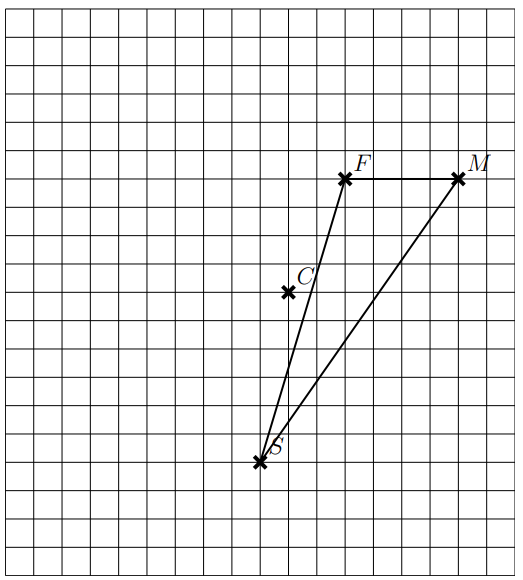
1. Construire par symétrie de centre U, l’image du cercle de centre W passant par X.

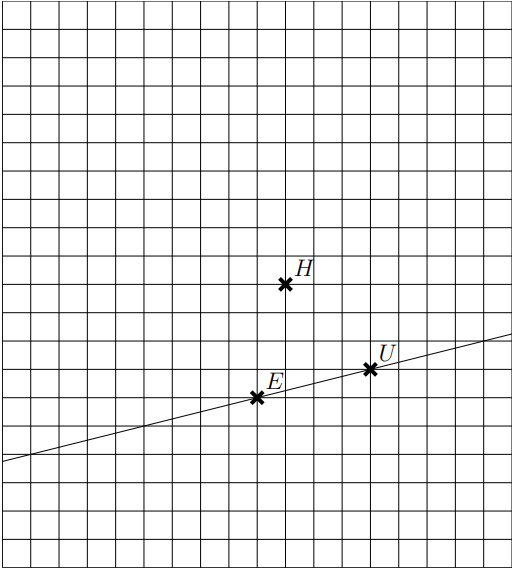
2. Construire par symétrie de centre H, l’image de la droite (EU).

3. Construire par symétrie de centre C, l’image du triangle FMS.

Exercice 5 **

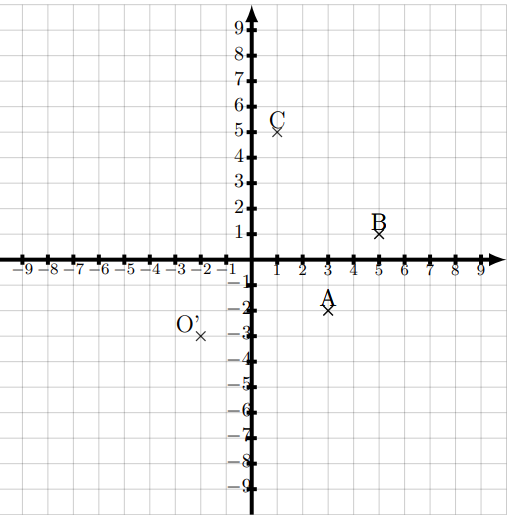
a. Donner les coordonnées de l’image de A par la symétrie de centre O.
b. Donner les coordonnées de l’image de B par la symétrie de centre A.
c. Donner les coordonnées de l’image de C par la symétrie de centre B.

Exercice 6 **

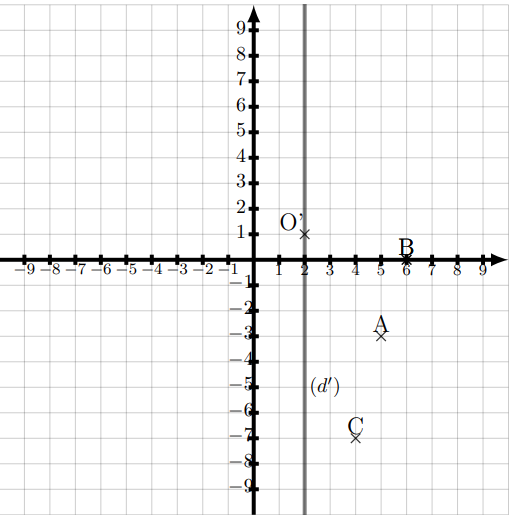
a. Donner les coordonnées de l’image de A par la symétrie de centre O’.
b. Donner les coordonnées du symétrique de B par rapport à la droite (d’).
c. Donner les coordonnées de l’image de C par la symétrie de centre B.

Exercice 7 ***

a. Donner le numéro de l’image de la figure 2 dans la symétrie de centre A.
b. Donner le numéro de l’image de la figure 4 dans la symétrie de centre A.
c. Donner le numéro de l’image de la figure 12 dans la symétrie de centre A.

Exercice 8 ***

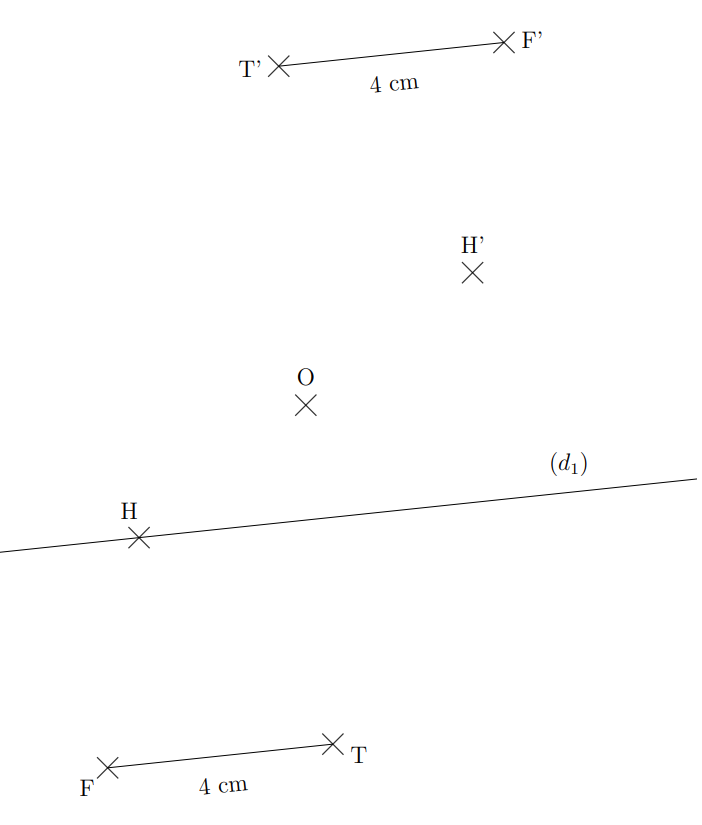
1. Les points F’, T’et H’ sont les images respectives de F, T et H par la symétrie de centre O.
La droite (d1) est parallèle au segment [F T] et passe par le point H.
Compléter l’image de la droite (d1) par la symétrie de centre O en utilisant les propriétés de conservation de la symétrie centrale et en justifiant ses démarches.

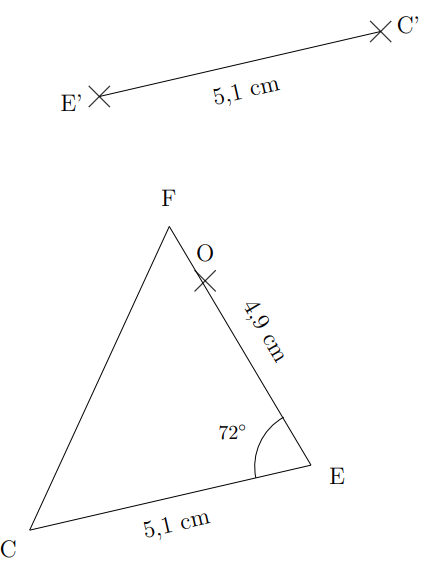
Les points C’et E’ sont les images respectives de C et E par la symétrie de centre O. L’angle CÊF d mesure 72 °.
Compléter l’image du triangle CEF par la symétrie de centre O en utilisant les propriétés de conservation de la symétrie centrale et en justifiant ses démarches.

Exercice 9 ***

Pour chacun de ces panneaux de signalisation, indiquer s’il a des axes de symétrie et/ou un centre de symétrie.

Série 2 : symétrie de figures par rapport à un point

Pages : 1 2