Le théorème de Pythagore et sa réciproque
1-Utiliser l’égalité de Pythagore
Fiche (Leçon) : Utiliser l’égalité de Pythagore

1-Utiliser la racine carée
Définition de la racine carré
Le nombre positif qui, élevé au carré, donne le nombre a s’appelle la racine carrée de a. On le note √ .
Exemple : Il y a deux nombres qui, élevés au carré, donnent 25 : ce sont 5 et -5
car 52 = 25 et (-5)2 = 25. √ 25 est le nombre positif, c’est-à-dire 5.
Règles
Pour tout nombre positif a, on a √ a² = a et ( √ a)²=a
Définition d’un carré parfait
Un carré parfait est le carré d’un nombre entier.
Exemple : Voici la liste des 15 premiers carrés parfaits :
1²=1 ; 2²=4 ; 3²=9 ; 4²=16 ; 5²=25 ; 6²=36 ; 7²=49 ; 8²=64 ; 9²=81 ; 10²=100 ; 11²=121 ; 12²=144 ; 13²= 169 ; 14²=196 ; 15²=225.
2-Enoncé du théorème de Pythagore
Dans un triangle rectangle, le plus grand côté est appelé hypoténuse.
C’est le côté opposé à l’angle droit.
Dans le triangle ABC rectangle en B, l’hypoténuse est [AC].
[BA] et [BC] sont les côtés de l’angle droit.
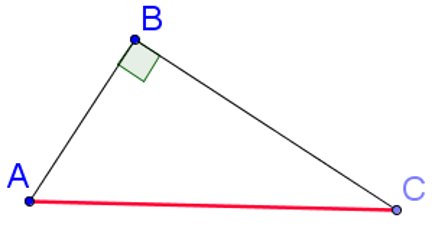
Théorème de Pythagore (le sens direct)
Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des côtés de l’angle droit.
Si ABC rectangle en B alors BA² + BC² = AC²
3-Calculer une longueur avec le théorème de Pythagore
Exemple 1: (calcul de longueur de l’hypothénuse)
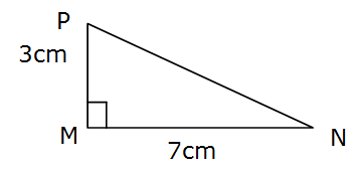
Le triangle MNP est rectangle en M tel que MN = 7 cm et MP = 3 cm.
Calculer la longueur NP.
On cherche l’hypoténuse
Solution
Le triangle MNP est rectangle en M.
D’après le théorème de Pythagore, on a NP² = MP² + MN²
NP² = 3² + 7²
NP² = 9 + 49 = 58
Donc NP = √ 58 ≈ 7, 6 cm (valeur arrondie au dixième du centimètre)
Exemple 2: (calcul de longueur d’un côté de l’angle droit)
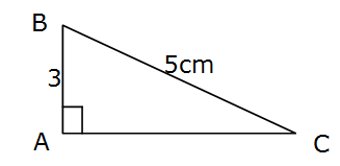
Le triangle ABC est rectangle en A tel que AB = 3 cm et BC = 5 cm.
Calculer la longueur AC.
On cherche un côté de l’angle droit
Solution
Le triangle ABC est rectangle en A, dD’après le théorème de Pythagore, on a :
BC² = AB² + AC²
AC² = BC² – AB²
AC² = 5² – 3²
AC² = 25 – 9 = 16
AC = √ 16 = 4 cm
4-Démontrer qu’un triangle est rectangle avec le théorème de Pythagore
Quand on connait les 3 longueurs des côtés d’un triangle, on peut savoir s’il est rectangle ou non.
Réciproque et autre formulation du théorème de Pythagore
Soit un triangle ABC dans lequel [AB] est le plus grand côté.
Si AB² = AC²+ BC² alors d’après la réciproque du théorème de Pythagore ce triangle est rectangle en C .
Si AB² ≠ AC²+ BC² alors l’égalité de Pythaogore n’est pas vérifiée et par conséquent ce triangle n’est pas rectangle.
Exemple 1:
Le triangle EFG est tel que EF = 3 cm, EG = 3,5 cm et FG = 4,5 cm.
Le triangle EFG est-il rectangle ?
Solution :
Dans le triangle EFG, [FG] est le plus grand côté.
FG² = 4,5² = 20,25 EF² + EG² = 3² + 3,5² = 9 + 12,25 = 21,25
FG² ≠ EF² + EG² (l’égalité de Pythagore n’est pas vérifiée) donc le triangle EFG n’est pas rectangle.
Exemple 2:
AIB est un triangle tel que AI = 2,4cm, IB = 4cm et AB = 3,2cm.
Démontrer que le triangle AIB est rectangle.
Solution
Dans le triangle AIB, [BI] est le plus grand côté.
BI² = 4² = 16 AB² + AI² = 3,2² + 2,4² = 10,24 + 5,76 = 16
On remarque que BI² = AB² + AI² donc d’après la réciproque du théorème de Pythagore, le triangle AIB est rectangle en A.