Un peu d’histoire

Pour découvrir la naissance de l’Algèbre.

Le calcul littéral ou algébrique apparait au 16e siècle avec les travaux de François Viete (1540-1603) puis et surtout avec ceux de René Descartes (1596-1650).

I-Activité

On souhaite tracer un rectangle dont la longueur est quatre fois plus grande que sa largeur.

1-Comment procéder ?

2-Donner l’expression de son périmètre et de son aire.

II- Simplifier une expression littérale

a- Rappel

Une expression littérale est une expression mathématique qui comporte une ou plusieurs lettres.

Ces lettres, appelées variables, désignent des nombres dont on ne connaît pas la valeur.

Par convention, pour simplifier et réduire une expression littérale, on peut :

  • supprimer le signe × et le facteur 1 devant une lettre ou une parenthèse ;
  • multiplier les lettres identiques entre elles en utilisant la notation de puissance ;
  • ajouter ou soustraire les termes de même nature. En revanche, on ne peut pas ajouter ou soustraire des termes de natures différentes.

Exemple

  • 0 × a = 0a = 0
  • 1 × a = 1a = a
  • 1 × (a + b) = a + b
  • 1+ (a + b) = 1+ a + b 
  • 1− (a + b) = 1− a − b 
  • a × b = ab
  • a × a = a ² (qui se lit « a au carré »)
  • a × a × a = a³ (qui se lit « a au cube »).
  • c × 3 = 3c (le nombre s’écrit toujours devant la lettre)
  • (2 + 𝑥) × (3 − y) = (2 + 𝒙) (3 − y)

Remarque : On ne peut pas supprimer le signe × entre deux nombres : 2 × 3 ≠ 23

Application

Simplifie l’expression suivante en supprimant les signes  ×  lorsque c’est possible :
A = 5 × 𝑥 + 7 × (3 × 𝑥 + 2 × 4)

Correction

A = 5 × 𝑥 +7 × (3 × 𝑥 +2 × 4)

A = 5𝑥 + 7(3 𝑥 + 8)

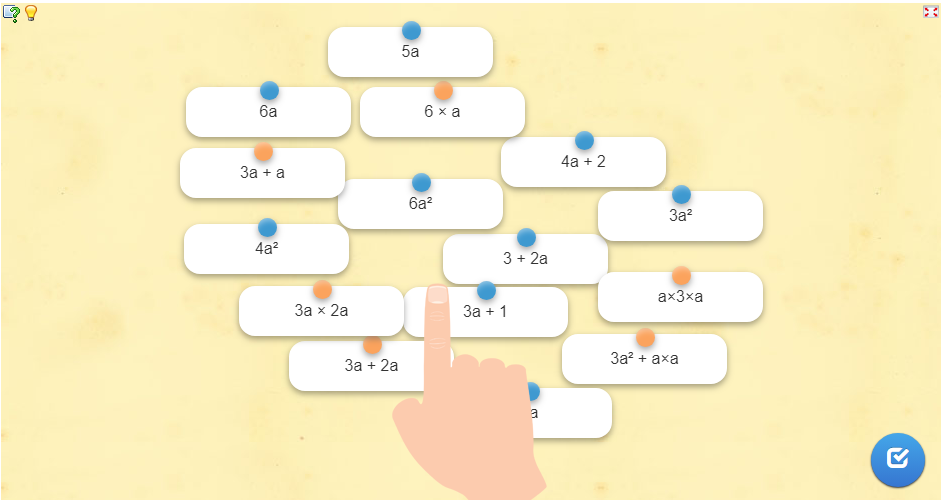
Entraine toi !

Calcul littéral-Partie1- conventions

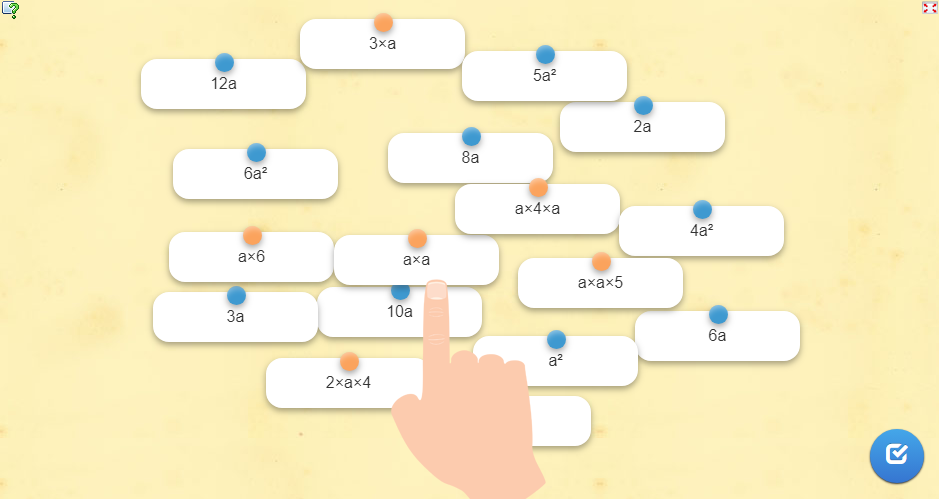
Calcul littéral-Partie2- Des additions et des multiplications

Revoir la simplification en vidéo

b- Réduire l’écriture d’une somme algébrique

Réduire, c’est effectuer tous les calculs possibles et appliquer les conventions d’écriture.​

Réduis A = 5𝑥 + 2𝑥 et B = 4𝑥 – 9𝑥

Correction

A = 5𝑥 + 2𝑥 = 7𝑥

B = 4𝑥 – 9𝑥 = – 5𝑥

c- Réduire une écriture d’une somme algébrique contenant des parenthèses

Définition

L’opposé d’une somme algébrique est égal à la somme des opposés de chacun de ses termes.

Exemple : L’opposé de (a + b – 2ab) est –a – b + 2ab.

 Remarque : Cette propriété permet de supprimer des parenthèses précédées d’un signe « – » dans une expression.

Exemple

Réduis l’expression :
G = 5𝑥² + (3𝒙– 4) – (2𝒙² – 3) + 2𝒙.

Correction

G = 5𝒙² + (3𝒙 – 4) – (2𝒙² – 3) + 2𝒙.

G = 5𝑥² + 3𝑥 – 4 – 2𝑥² + 3 + 2𝑥

G = 5𝒙² – 2𝒙² + 3𝒙 + 2𝒙 – 4 + 3

G = (5 – 2) 𝒙² + (3 + 2) 𝒙 – 1  

G = 3𝒙² + 5𝒙 – 1

Application

Réduire et simplifier les expressions suivantes autant que possible.
A= 7×𝒙×(−5)×𝒙

B = 8𝒙−12𝒙

C = 5𝒙−7+6𝒙

D = 3×5−7𝒙+3×2+12𝒙

E = 8−5𝒙²+6−5𝒙−2𝒙²

F = 7×𝒙×(−5)+𝒙×5×𝒙+11𝒙

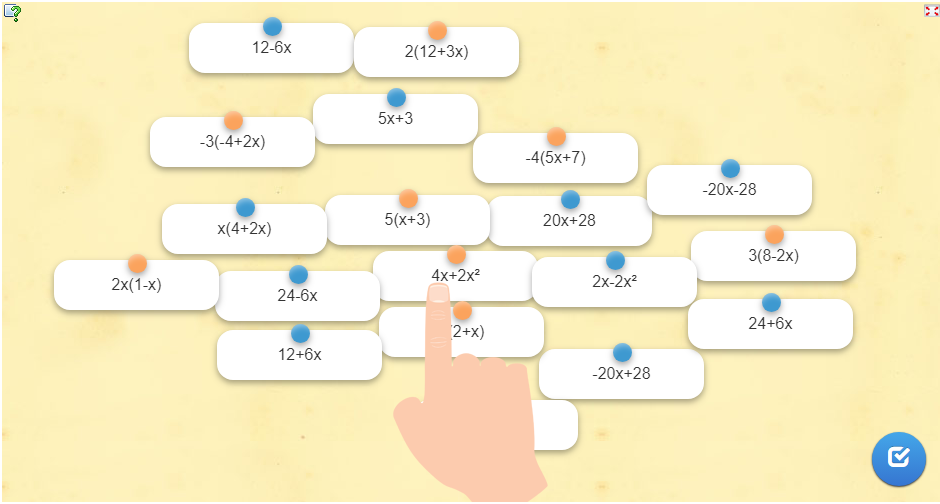
Jeu :

Essaye de trouver le code secret pour accéder au contenu d’un coffre.

III-Méthode pour démontrer que deux expressions sont égales

Pour démontrer que deux expressions littérales sont égales pour tout nombre 𝒙, on peut transformer l’écriture de l’une pour obtenir l’écriture de l’autre.

Pour démontrer que deux expressions littérales ne sont pas égales pour tout nombre 𝒙, il suffit de trouver une valeur de 𝒙 pour laquelle les deux expressions ne sont pas égales.

Exemple 1

L’égalité suivante est-elle vraie ?
3- 8𝒙-1-2𝒙 = -10 𝒙 + 2

Commençons par réduire le premier membre de l’égalité :

3- 8𝒙-1-2𝒙 = 3-1-8𝒙-2𝒙 = 2- 10𝒙 =-10𝒙+2

Donc l’égalité est vraie pour tout nombre 𝒙.

Exemple 2

L’égalité suivante est-elle vraie ?
3𝒙+7= 4𝒙

Si 𝒙 = 0 alors 3𝒙+7 = 7 et 4𝒙 = 0

7 ≠ 0 donc 3𝒙 + 7 = 4𝒙 n’est pas vraie pour tout nombre 𝒙

IV-Vocabulaire

Le résultat d’une addition est une somme, le résultat d’une soustraction est une différence.

Les nombres qui interviennent dans une addition ou une soustraction sont les termes.

Le résultat d’une multiplication est un produit. Les nombres multipliés sont les facteurs.

Le résultat d’une division est un quotient.

La nature d’une expression comportant plusieurs opérations est déterminée par l’opération à effectuer en dernier.

• Factoriser, c’est transformer une somme (ou une différence) en un produit.​

• Développer, c’est transformer un produit en une somme (ou en une différence.)​

• Une expression est une somme si la dernière opération à effectuer est une addition.​

• Une expression est une différence si la dernière opération à effectuer est une soustraction.​

• Une expression est un produit si la dernière opération à effectuer est une multiplication.

Exemple

Déterminer si ces expressions sont des sommes, des différences, des produits ou des quotients.

3 × (7 + 𝒙) ÷ y

3 × (76 + 𝒙) ÷ y

2 × (𝒙 + 4)

2 × (𝒙 + 4) 2×(5−𝒙) + 3 × (8 + y)

V-Développer une expression à l’aide de la simple distributivité

Activité

k, a et b désignent des nombres.

1- Exprimer de deux manières différentes l’aire du rectangle ACDF.

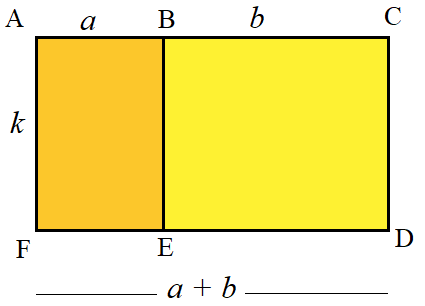
2- Exprimer de deux manières différentes l’aire du rectangle ABFE.

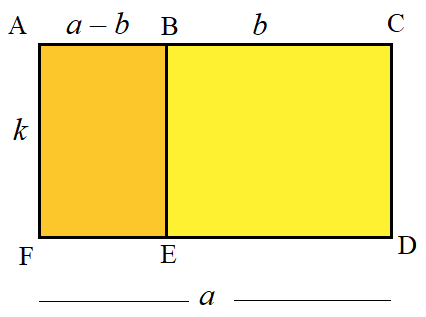
Bilan : propriété de la simple distributivité

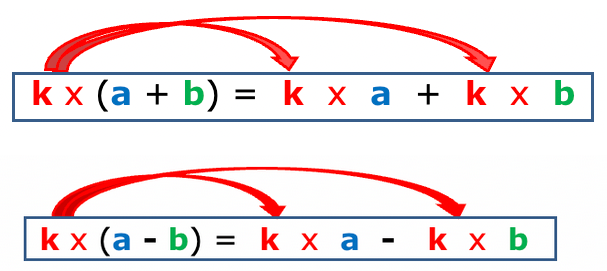
Exemple 1

13 × (13 + a) = 13 × 13 + 13 × a = 169 + 13a

Exemple 2

13 × (13 – a) = 13 × 13 – 13 × a = 169 – 13a

Exercice d’application :

Développer et réduire les expressions suivantes

A = 6(−3t − 7)

B = (4y − 5) ×3

C = (8c − 9) × (−3)

D= −3(−9t + 2)

Entraine toi !

Calcul littéral-déveloper avec la simple distributivité

 Calcul littéral : développer une expression-1

 Calcul littéral : développer une expression-2

Pour imprimer la leçon

Pages : 1 2 3