Construction de triangles

5-Activité
a- Expérimentation
Dans chaque cas, construire un triangle dont les longueurs sont les suivantes :
Triangle 1 : 8 cm ; 5 cm et 3 cm
Triangle 2 : 7 cm ; 6 cm et 4 cm
Triangle 3 : 4 cm ; 10 cm et 3 cm
b- Conjecture
Conjecturer la condition que doit vérifier la plus grande des trois longueurs pour pouvoir construire le triangle.

6-Inégalité triangulaire
a-Propriété
Quels que soient les points A, B et C, on a toujours :
AB + BC ⩾ AC
Exemple
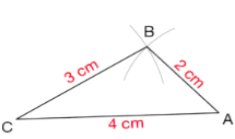
AB + BC ⩾ AC
2 + 3 ⩾ 4
b-Condition d’existence d’un triangle
Dans un triangle, la longueur du grand côté est inférieure à la somme des longueurs des 2 autres côtés.
Exemple :

Ce triangle ABC est constructible car 4 < 3 + 2 = 5 donc AC < AB + BC
c-Points alignés : condition d’appartenance à un segment
Si AC = AB + BC, alors B ∈ [AC], on dit alors que les points A, B, C sont alignés.
On dit aussi que le triangle ABC est aplati.
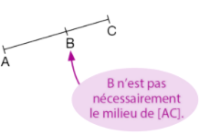
B ∈ [AC], (on lit : le point B appartient au segment [AC])
Pour revoir la leçon en vidéo
