Vitesse et grandeurs composées

1-Une grandeur quotient
Une grandeur quotient est une grandeur obtenue en effectuant le quotient de deux grandeurs.
Exemple : Vitesse moyenne
Dans un mouvement uniforme, la distance parcourue est proportionnelle à la durée du parcours.
Le coefficient de proportionnalité est appelé vitesse
moyenne. On a la formule :
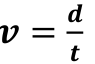
Elle s’exprime dans les mêmes unités que les deux grandeurs 𝑑 𝑒𝑡 𝑡 : si 𝑑 est exprimée en kilomètre et 𝑡 𝑒𝑛 ℎ𝑒𝑢𝑟𝑒 alors l’unité de vitesse est le “𝒌𝒊𝒍𝒐𝒎è𝒕𝒓𝒆 𝒑𝒂𝒓 𝒉𝒆𝒖𝒓𝒆” noté 𝑘𝑚/ℎ.
2-Calcul d’une grandeur composée
a : Calcul d’une distance
Exemple 1
Une voiture roule pendant 3h à la vitesse moyenne de 85 km/h.
Calculer la distance parcourue par la voiture.
Réponse

La voiture parcourt 85 km en 1 heure donc 255 km en 3 heures.
Il faut penser à faire une phrase pour répondre à la question, en n’oubliant pas les bonnes unités.
La voiture parcourt 255 km en 3 heures.
Exemple 2
Une moto roule pendant 2h 30 minutes à la vitesse moyenne de 60 km/h.
Calculer la distance parcourue par la moto.
Réponse
Attention, ici la principale difficulté est de convertir le temps qui est écrit en heure + minute en heure décimale (avec des virgules).
2h 30 minutes = 2,5 h en effet 30 minutes = une demi-heure = 0,5 heure

La moto parcourt 150 km en 2 heures 30 minutes.
b : Calcul d’une vitesse moyenne
Exemple 3
Un piéton rapide parcourt 2,7 km en 30 minutes. Calculer sa vitesse
moyenne en m/s.
Réponse
On veut la vitesse en m/s, il faut donc convertir avant de faire le calcul :
30 minutes = 1 800 secondes
2,7 km = 2 700 mètres. On en déduit donc la vitesse.

Ce piéton a une vitesse de 1,5 m/s.
Exemple 4
Un bateau met 45 minutes pour faire une traversée de 30 km.
Calculer sa vitesse moyenne en km/h.
Réponse
Attention, ici il faut convertir le temps qui est écrit en minutes en heure décimale (avec des virgules).
45 minutes = (45 : 60) heure = 0,75 heure.

Le bateau a une vitesse de 40 km/h
c : Calcul d’une durée
Exemple 5
Un camion roule sur 180 km à la vitesse moyenne de 75 km/h.
Calculer le temps mis par le camion en h min.
Réponse

Attention, 2,4 heures, ce n’est pas 2h40 ou 2h04 mais 2,4 h, Il faut reconvertir en heure + minutes.
Le camion met 2h 24 minutes pour parcourir 180 km à 75 km/h.
Exemple 6
Un véhicule roule sur 360 km sur l’autoroute à la vitesse moyenne de
96km/h. Calculer le temps mis par le véhicule en h min.
Réponse

Attention, 3,75 heures, ce n’est pas 3h75, Il faut reconvertir en heure + minutes.
Le véhicule met 3h 45 minutes pour parcourir 360 km à 96 km/h.
c : Conversions des unités de durée
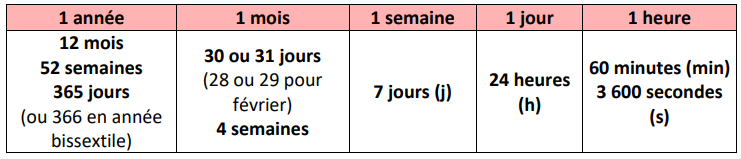
Convertir des heures, du système décimal (base 10) au système sexagésimal (base (60)
Pour convertir 4,35 h en heures entières et minutes :
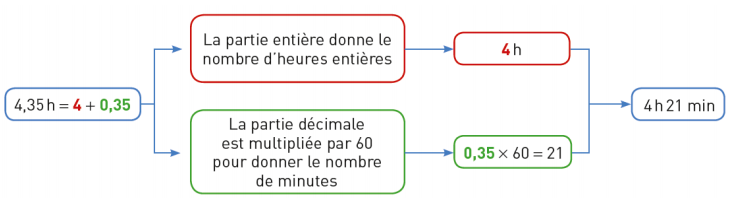
Exemple 7
Convertir des heures, du système décimal au système sexagésimal.
3,15 h = …………
12,89 h = ……….
0,34 h = …………
7,75 h = ………..
17,02 h = ………..
1,50 h = …………
Convertir des minutes en heures dans le système sexagésimal
Pour convertir 357 min en heures entières et minutes : je divise par 60 avec la calculatrice puis j’applique la méthode précédente.
357 : 60 = 5,95
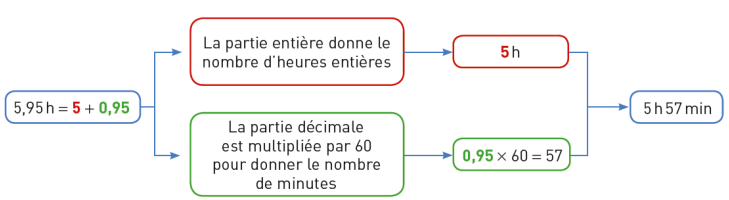
Exemple 8
Convertir des minutes en heures dans le système sexagésimal.
325 min = …………
1 287 min = ……….
36 min = ……………
875 min = ………..
1 704 min = ……….
145 min = …………
Convertir des heures, du système sexagésimal au système décimal
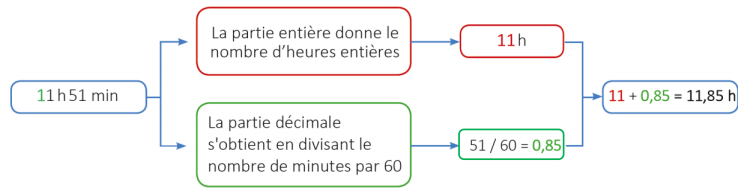
Pour convertir 11 h 51 min en écriture décimale :
Exemple 9
Convertir des heures, du système sexagésimal au système décimal.
3 h 45 min = ………..
13 h 12 min = ……….
1 h 25 min = …………
6 h 05 min = ………..
18 h 56 min = ……….
23 h 34 min = ……….
3-Application : calcul d’une échelle
Définition
Sur un plan dit « à l’échelle », les longueurs sont proportionnelles aux longueurs réelles.
Le coefficient obtenu en divisant les longueurs de la carte par les longueurs réelles, toutes exprimées dans la même unité, s’appelle échelle du plan.
Exemple 10
Sur un plan à l’échelle 1/5000 deux villes sont séparées de 12 𝑐𝑚. Quelle distance sépare ces deux villes dans la réalité ?
Réponse

La distance qui sépare ces deux villes dans la réalité est égale 60 000 cm = 600 m = 0,6 km
Exemple 11
Une carte est à l’échelle 1/25000 . Quelle longueur sur la carte représente une distance dans la réalité de 9 𝑘𝑚 ?
Réponse

La longueur sur la carte qui représente la distance de 9 𝑘𝑚 est égale 36 cm.
Exemple 12
𝟔 𝒄𝒎 sur une carte représentent 𝟏𝟓 𝒌𝒎 dans la réalité. Quelle est l’échelle de cette carte ?
Réponse

L’échelle de cette est de 1/250 000