Fonctions linéaires et fonctions affines

I-Fonctions affines
1) Définition et propriétés
Une fonction affine est de la forme ƒ : 𝑥 ↦ a𝑥 + b
a est le coefficient directeur, b est l’ordonnée à l’origine.
Exemple 1
Pour a = 2 et b = –3
g est la fonction affine définie par g : 𝑥 ↦ 2𝑥 – 3
• L’image de 𝑥 par la fonction g est g(𝑥) = 2𝑥 – 3
• L’image de 5 par la fonction g est g(5) = 2×5 – 3 = 7
Exemple 2
Entourer les fonctions affines et déterminer les coefficients a et b.

Remarque
Si b = 0, la fonction est une fonction linéaire.
Si a = 0, la fonction est une fonction constante.
2) Représentation graphique d’une fonction affine
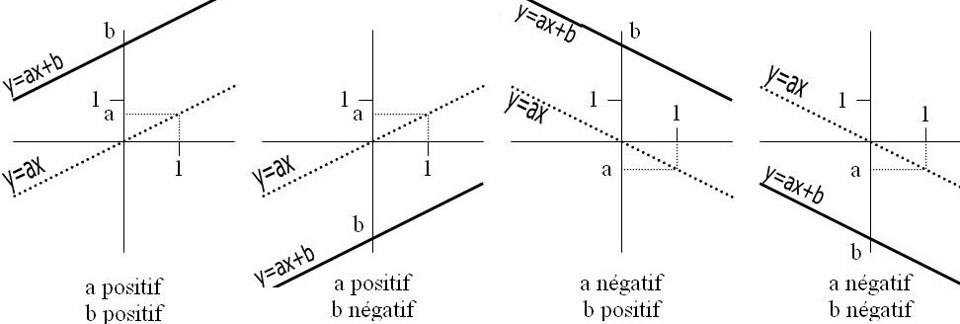
La représentation graphique d’une fonction affine est une droite qui, généralement, ne passe pas par l’origine du repère.
Pour la tracer, il suffit de connaitre 2 points (et un 3e pour vérifier).
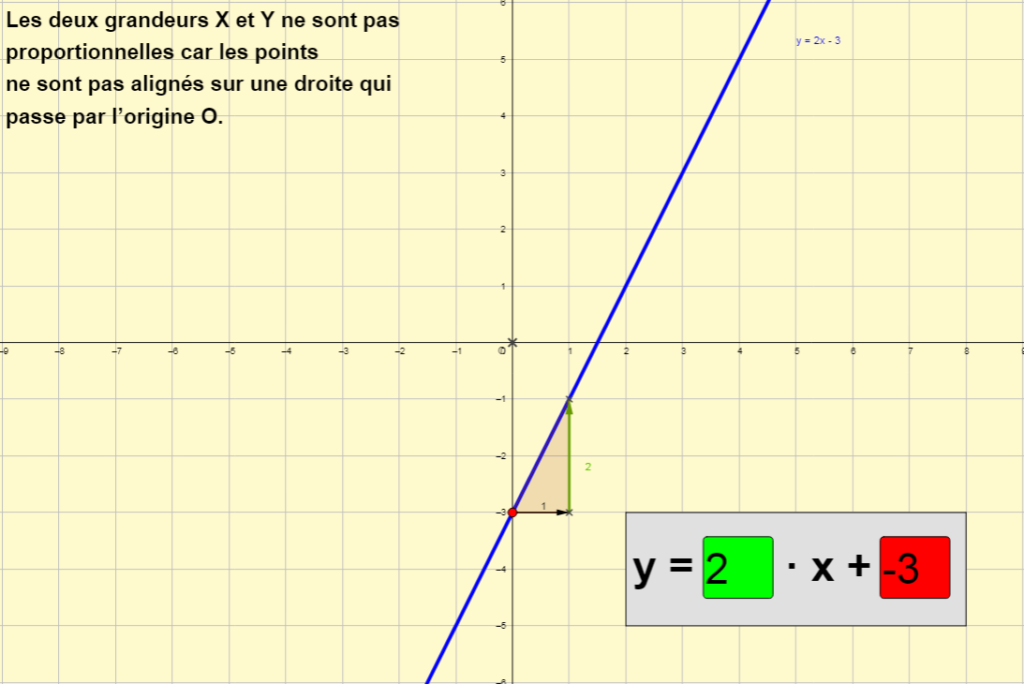
b est l’ordonnée à l’origine, l’ordonnée où la droite coupe l’axe vertical.
Remarque
Dans le cas général (si b ≠ 0), une fonction affine NE représente PAS une situation de proportionnalité.
Deux droites ayant le même coefficient directeur sont parallèles.

L’essentiel à retenir
