Fonctions linéaires et fonctions affines
Activité


Rappels :
Une fonction est un processus (ou une « machine à calculer » qui permet d’obtenir un nombre à la sortie « en fonction » du nombre choisi en entrée.
Le nombre obtenu « à la sortie » s’appelle l’image.
Le nombre « à l’entrée » s’appelle l’antécédent.
Notation :
Pour la fonction ƒ, l’image de 𝑥 est ƒ(𝑥), on note ƒ : 𝑥 ↦ƒ(𝑥)
Exemple :
h : 𝑥 ↦𝑥 – 3, on a h(𝑥) = 𝑥 – 3
L’antécédent de 1 par la fonction h est 4.
L’image de -1 par la fonction h est -4.
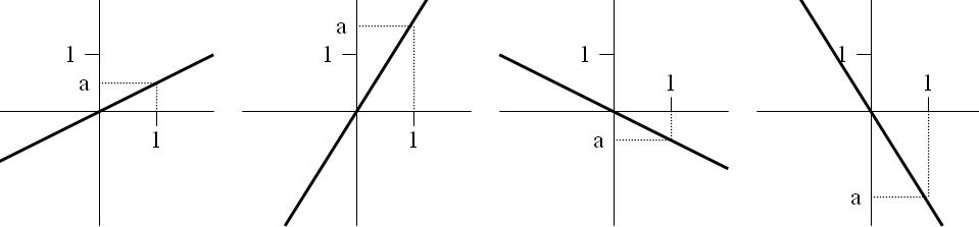
I-Fonctions linéaires
1) Définition et propriétés
Une fonction linéaire représente une situation de proportionnalité.
Son expression algébrique est de la forme : 𝑥 ↦ a𝑥 où a est le coefficient directeur.
Les tableaux de valeurs associés à une fonction linéaire sont des tableaux de proportionnalité, leur coefficient de proportionnalité est a.
Exemple 1
g est la fonction linéaire de coefficient 2.
• On note : g(𝑥) = 2𝑥
• L’image de 𝑥 par la fonction g est 2𝑥.
• L’image de 5 par la fonction g est g(5) = 2×5 = 10
Exemple 2
Entourer les fonctions linéaires et déterminer leurs coefficients.
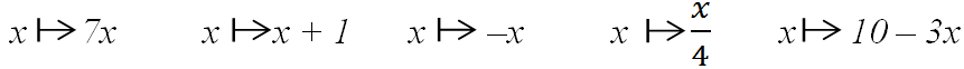
La fonction définie par 𝑥 ↦ 𝑥 + 1 n’est pas une fonction linéaire car elle n’est pas sous la forme 𝑥 ↦ a𝑥.
La fonction définie par 𝑥 ↦ 10 – 3𝑥 n’est pas une fonction linéaire car elle n’est pas sous la forme 𝑥 ↦ a𝑥.
2) Représentation graphique d’une fonction linéaire
La représentation graphique d’une fonction linéaire est une droite passant par l’origine du repère.
Pour la tracer, il suffit de connaitre 2 points (et un 3e pour vérifier).
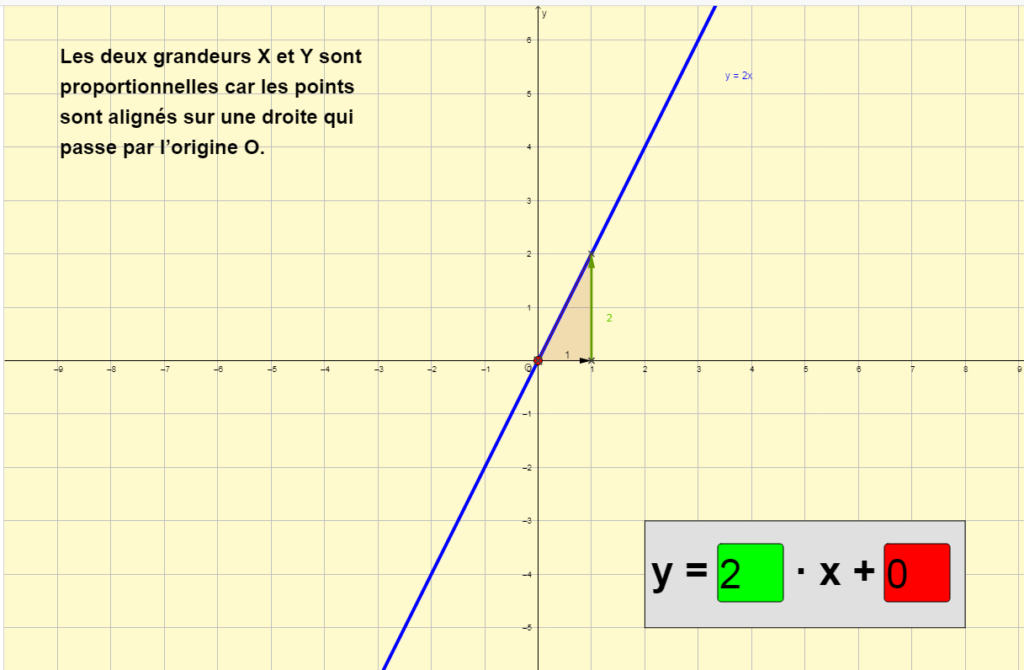
Exemple 3
a est aussi appelé la pente de la droite.