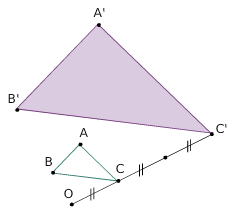
Homothétie-Triangles semblables
Exercices

Exercice1
Construire un carré ABCD de côté 3 cm.
Placer un point O à l’extérieur du carré.
Construire l’image A’B’C’D’ du carré ABCD par l’homothétie de centre O et de
rapport -0.5.
Exercice 2
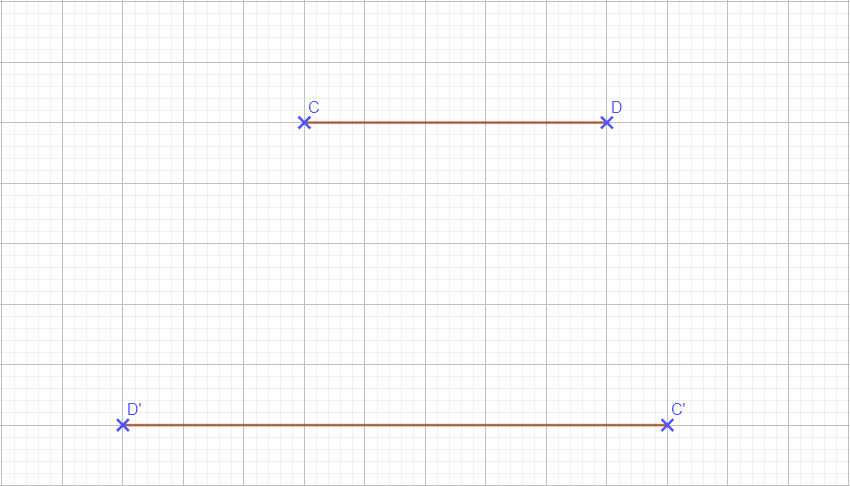
a) Reproduire la figure ci-dessus.
C’ est l’image de C par une homothétie h de centre I et de rapport k.
D’ est l’image de D par cette même homothétie h.
b) Construire le centre I et déterminer le rapport k de cette homothétie en
justifiant.
c) Ecrire les égalités faisant intervenir des longueurs des segments et le rapport k de l’homothétie.
d) Que peut-on dire des triangles ICD et IC’D’ ?
Exercice 3
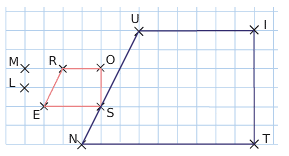
Par quelle homothétie,
- le quadrilatère NUIT est-il l’image du quadrilatère ROSE ?
- le quadrilatère ROSE est-il l’image du quadrilatère NUIT ?
Exercice 4
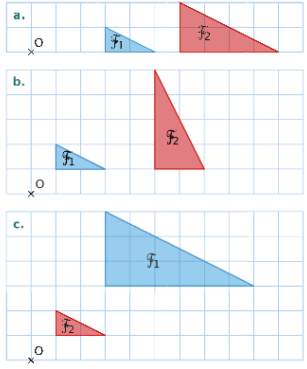
Dans les cas ci-dessous, indiquer si la figure est l’image de la figure
par une homothétie de centre O.
Si c’est le cas, préciser son rapport.
Exercice 5
Sur la figure suivante, ABC est un triangle rectangle en A tel que AB= 6 cm et AC= 8 cm.
A’B’C’ est l’image de ABC par une homothétie de centre O.
1. Donner en justifiant, le rapport de cette homothétie.
2. Quelle est la nature du triangle A’B’C’ ?
3. Calculer le périmètre puis l’aire du triangle ABC.
4. En déduire le périmètre puis l’aire du triangle A’B’C’.