Statistiques

Activité 1
Dans une entreprise, on a étudié l’âge des 125 salariés.
Les résultats de cette étude sont donnés dans le tableau suivant :
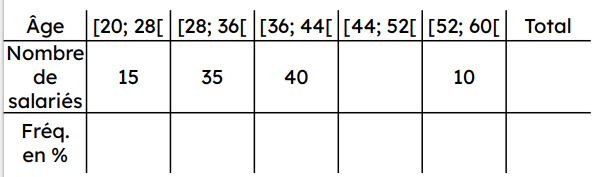
1- Reproduire et compléter le tableau.
2- Tracer l’histogramme des effectifs.
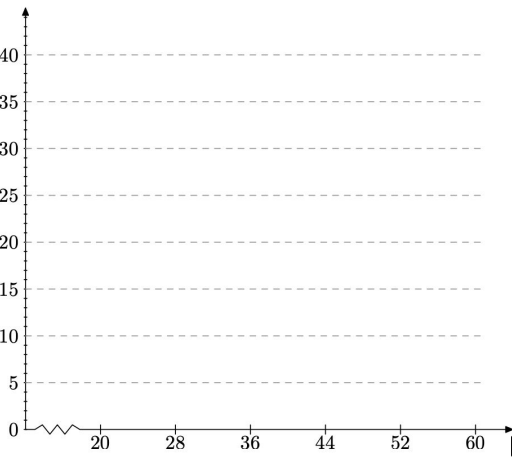
3- a. Combien de salariés ont moins de 44 ans ?
3- b. Combien de salariés ont 36 ans et plus ?
3- c. Quel pourcentage de salariés a entre 52 ans et 60 ans ?
Coup de pouce :
Un histogramme permet de représenter une série de données regroupées en classes. Chaque classe est représentée par un rectangle dont l’aire est proportionnelle à l’effectif.
Si toutes les classes ont la même amplitude, les rectangles ont la même largeur et leur hauteur est alors proportionnelle à l’effectif de la classe qu’ils représentent.
I- Calculer une fréquence
La fréquence d’une valeur est le quotient de l’effectif de la valeur par l’effectif total, elle est comprise entre 0 et 1.
Elle peut être exprimée sous forme décimale ou fractionnaire.
Fréquence =

Fréquence en % =
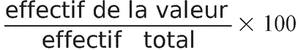
Exemple :
La fréquence de la valeur 15 est 8/15 soit une fréquence
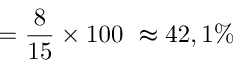
II- Calculer une moyenne simple et pondérée

Activité 2
Lors du dernier sondage, voici les réponses des élèves à la question suivante : « Combien de temps dure ton trajet pour aller au collège ? »
20 ; 15 ; 12 ; 15 ; 10 ; 7 ; 15 ; 7 ; 5 ; 15 ; 3 ; 2 ; 5 ; 15 ; 10 ; 10 ; 15; 15 ; 15.
On appelle cette liste de données une série statistique.
1- Calculer l’effectif total de cette série.
2- Calculer la durée du trajet moyen.
3- Regrouper les données précédentes dans un tableau à effectifs.
Si une valeur apparait 3 fois alors son effectif est égal à 3.

4- Calculer la durée du trajet moyen en utilisant le tableau à effectifs.
Définition de la moyenne simple
La moyenne d’une série de données numériques est égale au quotient de la somme de ces données par l’effectif total.
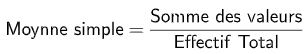
Définition de la moyenne pondérée
La moyenne pondérée d’une série de données numériques est égale au quotient de la somme des produits de chaque donnée par son effectif, divisée par l’effectif total.
Moyenne pondérée :
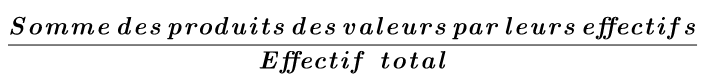
III- Calculer la médiane d’une série statistique
Définition :
La médiane d’une série statistique est la valeur qui partage la série en deux parties de même effectif.
Au moins 50 % des valeurs de la série sont supérieures ou égale à la médiane.
Au moins 50 % des valeurs de la série sont inférieures à égale la médiane.
Exemple 1 : (cas d’un effectif total impair)
3 ; 5 ; 5 ; 11 ; 2 ; 0 ; 12
Calculer la médiane de la série ci-dessus.
Solution
On range les valeurs dans l’ordre croissant
0 ; 2 ; 3 ; 5 ; 5 ; 11 ; 12
Effectif total = 7, on cherche ensuite la position de la valeur médiane
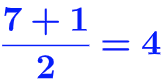
La médiane est la 4ème valeur de la série (rangée) donc la médiane est égale à 5.
Exemple 2 : (cas d’un effectif total pair)
-12 ; -2 ; 0 ; 2 ; 5 ; 6 ; 8 ; 11
Calculer la médiane de la série ci-dessus.
Solution
On range les valeurs dans l’ordre croissant
N= 8 , on cherche ensuite la position de la valeur médiane.
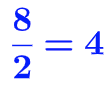
La médiane est la valeur qui se trouve entre la 4ème et la 5ème position donc la médiane est égale :
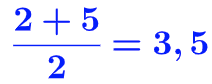
IV- Calculer l’étendue d’une série statistique
L’étendue d’une série statistique est la différence entre la valeur maximale et la valeur minimale.
Calculons l’étendue de la série précédente
E = 11 – (-12) = 23