Puissances

Activité : Découvrir la notation des puissances

Le 1er avril, Sonia entend à la radio que son groupe préféré va donner un concert dans sa ville.
Elle envoie immédiatement un message à trois copines pour les informer de cet évènement.
Le 2 avril, chacune des trois copines envoie à son tour un message à trois autres copines pour les avertir. Et ainsi la nouvelle se propage rapidement : dès qu’une personne l’apprend, elle en informe trois autres le
lendemain.
1- Combien de nouvelles personnes apprennent l’information le 2 avril ? le 3 avril ? le 4 avril ? le 5 avril ?
2- Quel calcul permet de trouver combien de nouvelles personnes apprennent l’information le 10 avril ? Écrire seulement le calcul sans l’effectuer.
3- Quel calcul permet de trouver combien de nouvelles personnes apprennent l’information le 1er mai ? Écrire seulement le calcul sans l’effectuer.
4- Que peut-on dire de ce dernier calcul ? Quel codage peut-on proposer pour le raccourcir ?
I- Comprendre la notation de puissance
1. Puissances d’exposant positif
Définition :
Soit a un nombre relatif et n un entier naturel.
On appelle puissance de a exposant n le nombre défini par :
aⁿ= a × a × a ×…× a (n fois le facteur a)
Exemples :
- 7³ = 7 × 7 × 7 = 343
- (−5)⁴ = (−5) × (−5) × (−5) × (−5) = 625
Remarques :
a² se lit « a au carré » et a³ se lit « a au cube ».
a⁰ = 1 et a¹ = a par convention.
0⁰ n’existe pas.
2. Puissances d’exposant négatif.
Définition :
Si a est un nombre relatif et n un entier, l’inverse de aⁿ est donné par :

Exemples :
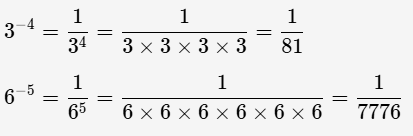
Remarque :
On peut dire aussi qu’une puissance d’exposant négatif est toujours l’inverse d’une puissance d’exposant positif.
II- Propriétés générales
Il est indispensable de connaître ses propriétés et de les maîtriser.
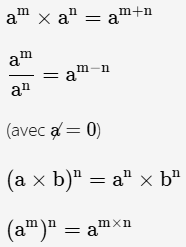
Exemples :
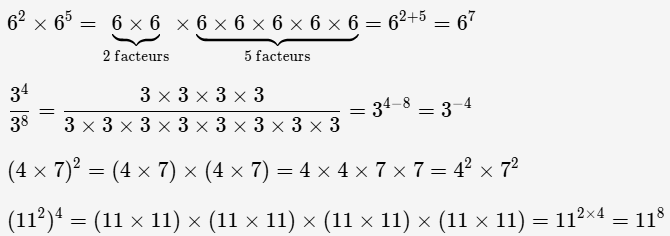
III- Cas particulier : les puissances de 10
La notation puissance est très utile dans l’écriture des nombres très grands ( comme les distances entre les planètes) et les très petits nombres (comme la taille de molécules ou d’atomes).

Activité : Découvrir les puissances de 10
Toutes les définitions, remarques, propriétés ou exemples cités plus haut sont encore valables lorsque l’on parle de puissances de 10.
1. Puissances de 10 d’exposant positif
Exemples :
10⁴ = 10 × 10 × 10 × 10 =10 000
La particularité ici est que le résultat de 10⁴ s’écrit comme un 1 suivi de quatre zéros.
Et cela se vérifie pour n’importe quelle autre puissance de 10 d’exposant positif :
10⁶ = 10 × 10 × 10 × 10 × 10 × 10 = 1000 000
10⁹ = 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 1000 000 000
10ⁿ s’écrit avec un 1 suivi de n zéros !
2. Puissances de 10 d’exposant positif
Examinons maintenant les puissances de 10 négatives.
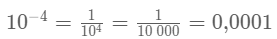
On remarque que 10-⁴ s’écrit comme un nombre décimal composé de zéros avec un 1 placé en quatrième position derrière la virgule : 0,0001.
Exemples :
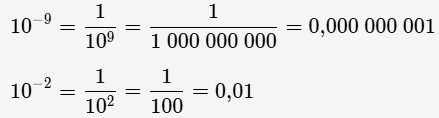
3. Écriture scientifique d’un nombre décimal
L’écriture scientifique d’un nombre décimal différent de 0 est l’écriture de la forme a × 10ⁿ où : a est un nombre décimal compris entre 1 et 10 (exclu) et n est un entier relatif.
Exercice :
Donner l’écriture scientifique du nombre 150 000 000 et du nombre 0,006 51.
Solution :
150 000 000 = 1,5 × 100 000 000 = 1,5 × 10⁸ car 100 000 000 = 10⁸
0,006 51= 6,51 × 0,001= 6,51 × 10 −³ car 0,001=10 −³
4. Les notations avec préfixes
On peut utiliser certains préfixes pour simplifier les noms et écritures des puissances de 10.
Nous en utilisons régulièrement dans notre vie quotidienne : kilo, méga, centi…
Ils sont résumés dans le tableau suivant :

Exemples :
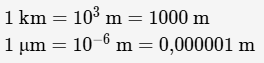
Exercice :
Utilisez la notation scientifique pour donner un ordre de grandeur de la dimension en mètre (m), de chaque objet.
- Grain de sable : 0,000 232 m
- Fil d’une toile d’araignée : 6 690 nm
- Particule de fumée de tabac : 0,27 μm
Solution :
- Grain de sable :
0,000 232 m = 2,32 × 0,000 1 m = 2,32 × 10−⁴ m - Fil d’une toile d’araignée :
6 690 nm = 6 690 × 10−⁹ m = 6,69×10³ × 10−⁹ m = 6,69 × 10−⁶ m - Particule de fumée de tabac :
0,27 μm = 0,27 × 10−⁶ m = 2,7 × 10−¹ × 10−⁶ m = 2,7 × 10−⁷ m