Probabilités

I : Définition d’une expérience aléatoire
Une expérience aléatoire est une expérience renouvelable à l’identique, dont les résultats possibles sont connus sans qu’on puisse déterminer lequel sera réalisé.
Exemples :

Les résultats possibles sont : 1, 2, 3, 4, 5 ou 6.

Les résultats possibles sont : Pile ou Face.

Nous avons 52 résultats possibles, 2 couleurs possibles et 4 motifs possibles (Trèfles, Carreau, Cœur et Piques).
II : Vocabulaire
Les résultats possibles s’appellent des issues.
Un événement est un ensemble d’issues.
Un événement élémentaire est un évènement qui ne contient qu’une seule issue.
La probabilité d’un événement estime la chance de se produire.
Exemple :
Les issues possibles d’un lancer de dé à six faces sont : { 1 ; 2 ; 3 ; 4 ; 5 ; 6}
Obtenir un nombre pair est un événement dont les issues possibles sont : { 2 ; 4 ; 6 }.
Obtenir un 6 est un événement élémentaire car il n’y a qu’une seule issue possible pour le réaliser.
III : Propriétés
Une probabilité est un nombre compris entre 0 et 1.
Plus la probabilité est proche de 1, plus l’événement a de chance de se réaliser.
Si elle est égale à 1, l’événement est appelé l’événement certain.
Un événement dont la probabilité est nulle est appelé l’événement impossible.
Exemple :
Obtenir un “7” avec un lancer de dé à 6 faces est un événement impossible car la probabilité de réaliser cet événement est nulle, P (Obtenir un “7”) = 0
Définition :
Une situation d’équiprobabilité est une expérience où toutes les issues ont la même chance de se produire.
Dans le cas d’un lancer de dé équilibré à six faces toutes les issues ont la même chance de se produire.
En cas d’équiprobabilité :
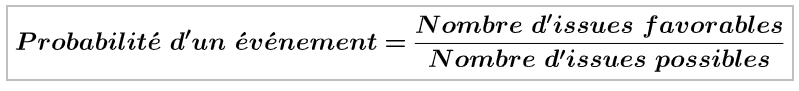
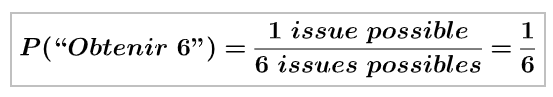
La somme de toutes les probabilités est toujours égale à 1.