Les solides : pyramide et cône de révolution

Exercices
Exercice 1
Dans chaque cas, reproduire la figure et la compléter pour représenter en perspective cavalière :
un cône de sommet A et de base de disque représenté.
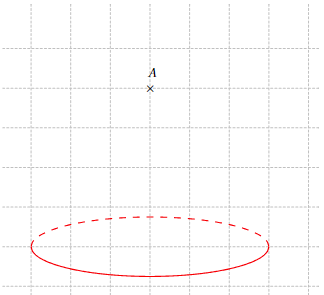
un cône de sommet S et de base le disque de rayon [OB].
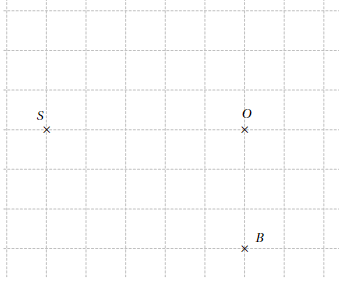
Exercice 2
Une lampe a la forme d’un cône de diamètre de base 7 cm et de hauteur 15 cm. Calculer le volume, en cm3, de cette lampe.
Exercice 3
Le cône en biscuit d’une glace a pour hauteur 12 cm et pour rayon 3 cm. Calculer le volume, en cm3, de ce cône
Exercice 4
Voici un cône et l’un de ses patrons. Le cercle de centre O et de rayon 5 cm et l’arc de cercle rouge ont la même longueur.
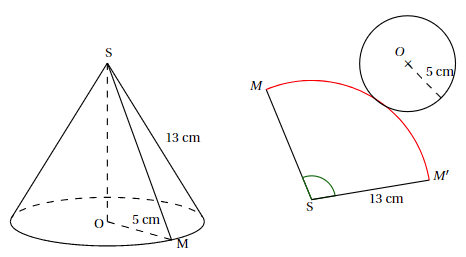
1. Exprimer en fonction de π la longueur :
• du cercle de centre O et de rayon 5 cm ;
• d’un cercle de rayon 13 cm.
2. La longueur d’un arc de cercle est proportionnelle à la mesure de l’angle qui l’intercepte. En utilisant un tableau de proportionnalité, déterminer la mesure de l’angle 𝑀Ŝ𝑀′. Donner une valeur approchée à l’unité près.
Exercice 5 (DNB Amérique du Nord juin 2016)
Sur l’altiport (aérodrome d’altitude) de la station de ski se trouve une manche à air qui permet de vérifier la direction et la puissance du vent.
Cette manche à air à la forme d’un tronc de cône de révolution obtenu à partir d’un cône auquel on enlève la partie supérieure, après section par un plan parallèle à la base.
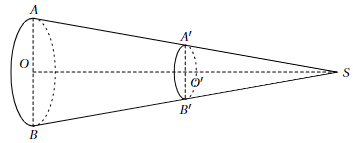
On donne : AB = 60 cm, A′B′ = 30 cm, SB′ = 240 cm.
O est le centre du disque de la base du grand cône de sommet S.
O′ milieu de [OS], est le centre de la section de ce cône par un plan parallèle à la base.
B’ appartient à la génératrice [SB] et A′ appartient à la génératrice [SA].
1. Démontrer que la longueur SB est égale à 480 cm.
2. Calculer la longueur SO. On arrondira le résultat au centimètre.
3. Calculer le volume d’air qui se trouve dans la manche à air.
On arrondira au centimètre cube
Exercice 6 (DNB Nouvelle Calédonie février 2020)
Les crevettes mangent des granulés qui sont stockés dans des réservoirs appelés silos.
Un silo est composé d’un cône de révolution surmonté d’un cylindre de même base de diamètre DC = 2,8 m. Le point A est le milieu du segment [DC]. La hauteur du cylindre est égale à 2,4 m.
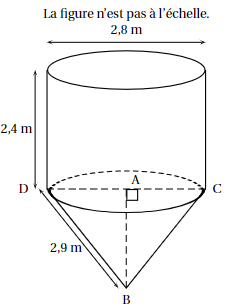
1. Calculer le volume du cylindre. Arrondir à l’unité.
2. Montrer que la hauteur AB du cône est environ de 2,5 m.
3. Calculer le volume du silo. Arrondir à l’unité.
4. L’aquaculteur commande 16 m3 de granulés pour crevettes.
Voici les informations dont il dispose :

Calculer le montant total (en F CFP) de la commande. Justifier la réponse
Exercice 7 (DNB Grèce juin 2019)
Dans le village de Jean, une brocante est organisée chaque année lors du premier week-end de juillet. Jean s’est engagé à s’occuper du stand de vente de frites. Pour cela, il fabrique des cônes en papier qui lui serviront de barquette pour les vendre.
Dans le fond de chaque cône, Jean versera de la sauce : soit de la mayonnaise, soit de la sauce tomate.
Il décide de fabriquer 400 cônes en papier et il doit estimer le nombre de bouteilles de mayonnaise et de sauce tomate à acheter pour ne pas en manquer.
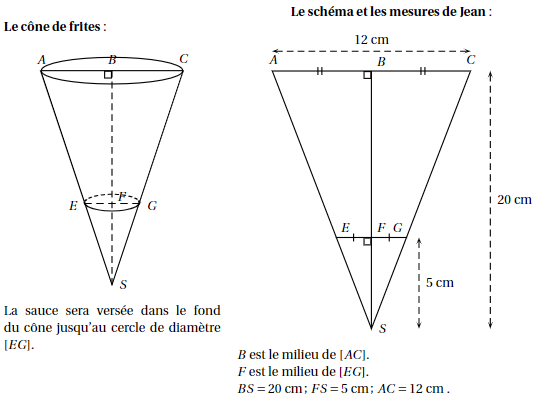
Voici les informations dont Jean dispose pour faire ses calculs :
Les acheteurs : 80 % des acheteurs prennent de la sauce tomate et tous les autres prennent de la mayonnaise.
Les sauces : La bouteille de mayonnaise est assimilée à un cylindre de révolution dont le diamètre de base est 5 cm et la hauteur est 15 cm.
La bouteille de sauce tomate a une capacité de 500 mL.
1. Montrer que le rayon [EF] du cône de sauce a pour mesure 1,5 cm.
2. Montrer que le volume de sauce pour un cône de frites est d’environ 11,78 cm3
3. Déterminer le nombre de bouteilles de chaque sauce que Jean devra acheter.