Les parallélogrammes

1) Vocabulaire :
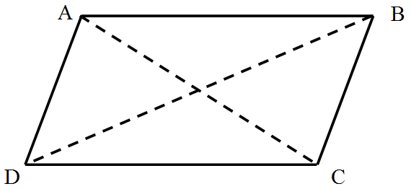
[AB] et [BC] sont des côtés consécutifs.
[AB] et [CD] sont des côtés opposés.
A et B sont des sommets consécutifs.
B et D sont des sommets opposés.
[AC] et [BD] sont les diagonales.
BĈD et BÂD sont des angles opposés.
2) Définition :
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles, deux à deux.
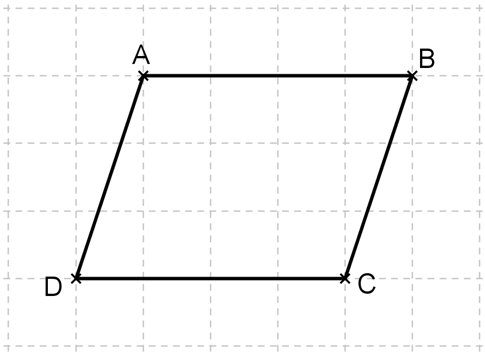
(AB) // (CD)
(AD) // (BC)
3) Propriétés :
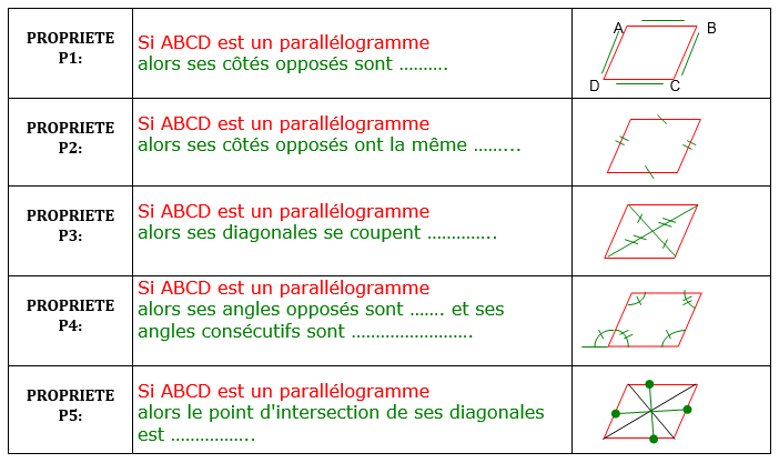
4) Propriétés réciproques :

5) Parallélogrammes particuliers :
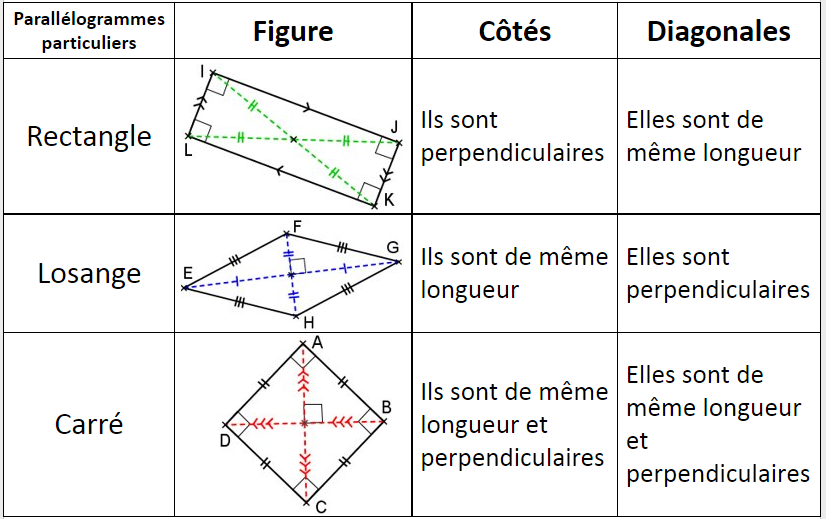
Activité 1 : reconnaître les parallélogrammes particuliers

6) Aire d’un parallélogramme :
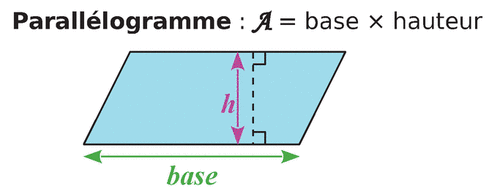
Exemple :
Détermine l’aire du parallélogramme MNOP.
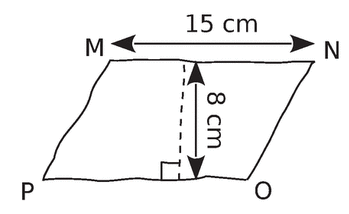
Aire de MNOP = Base x Hauteur = 15 x 8 = 120 cm²
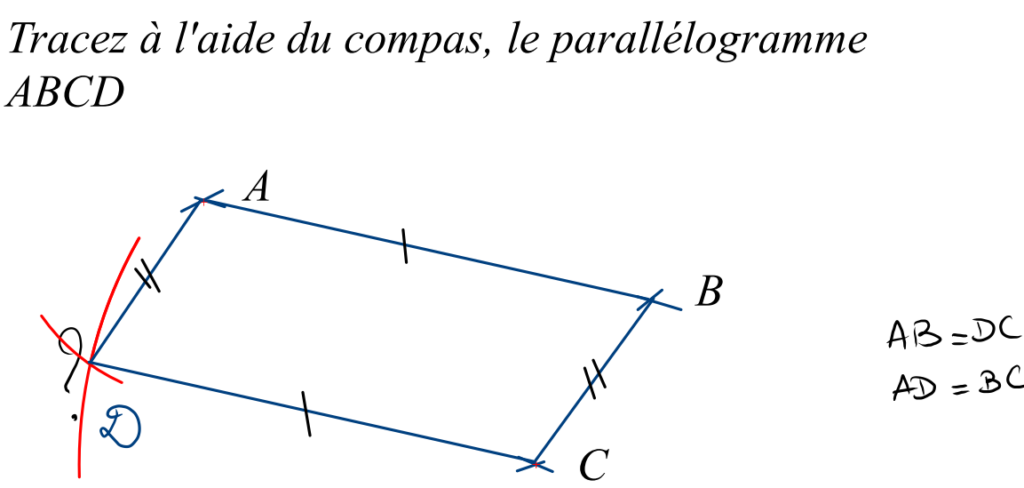
Activité 2 : tracer un parallélogramme à l’aide du compas uniquement.

La méthode pour tracer un parallélogramme à l’aide du compas est tout simplement l’application de la propriété suivante : Les côtés opposés d’un parallélogramme sont de même longueur.
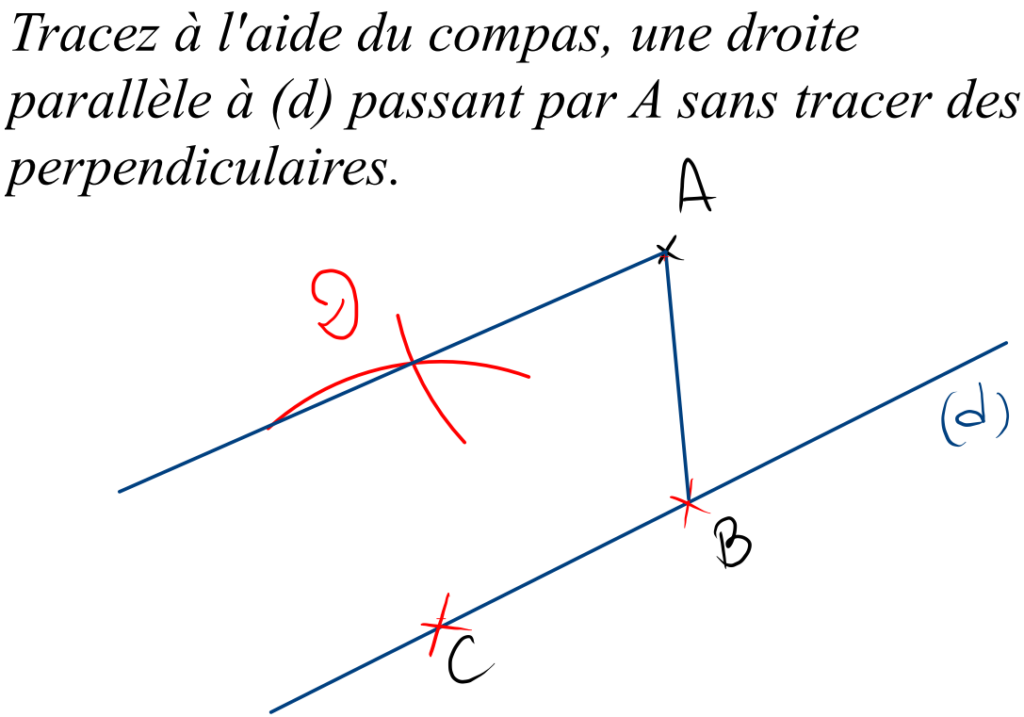
Activité 3 : tracer une parallèle à une droite passant par un point à l’aide du compas et sans passer par les perpendiculaires.

La méthode pour tracer une parallèle à une droite (d) passant par un point est celle du parallélogramme en plaçant deux point quelconques sur la droite (d).
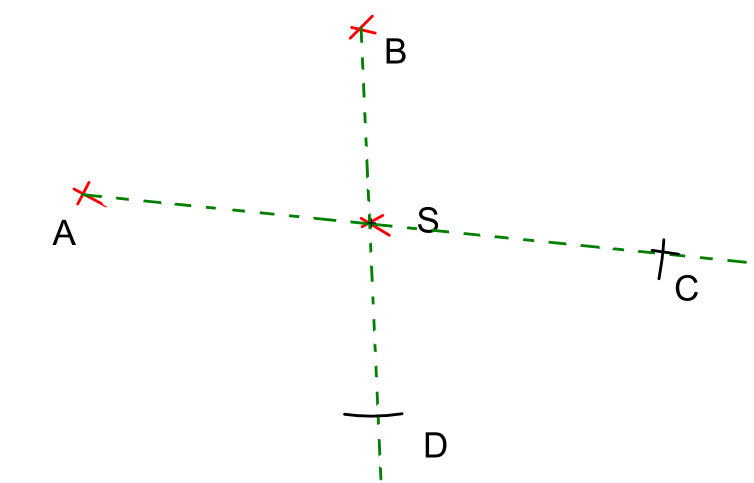
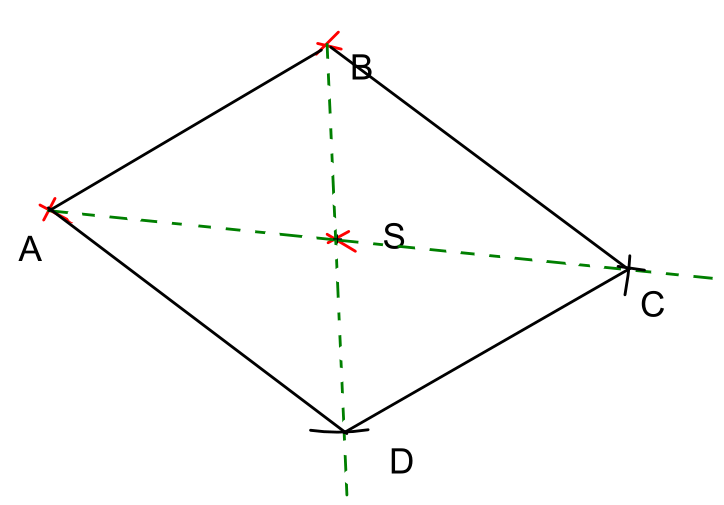
Activité 4 : tracer un paralléologramme connaissant deux sommets A et B et son centre

Activité 5 : définitions et propriétés des paralléologrammes particuleirs

Un rectangle est défini dans le dictionnaire de la façon suivante :
« Un rectangle est un quadrilatère dont les quatre angles sont droits. »
- Un quadrilatère qui possède deux angles droits est-il un rectangle ? Justifier.
- Dans une classe de CE2, une enseignante demande à ses élèves de compléter la phrase suivante : « Un rectangle est un quadrilatère dont … ».
Voici deux réponses proposées :
Élève A : « Un rectangle est un quadrilatère dont les côtés opposés sont de même longueur ».
Élève B : « Un rectangle est un quadrilatère dont les diagonales sont de même longueur ».
a. Préciser en quoi la réponse de l’élève A ne pourrait pas être admise comme définition mathématique du rectangle.
b. Préciser en quoi la réponse de l’élève B ne pourrait pas être admise comme définition mathématique du rectangle. - Quelle est la nature d’un rectangle dont les diagonales sont perpendiculaires ?
- En s’appuyant sur le codage du quadrilatère ci-après dessiné à main levée, préciser la nature du quadrilatère en question en justifiant la réponse.