Le théorème de Thalès et sa réciproque

Exercices
Exercice 1
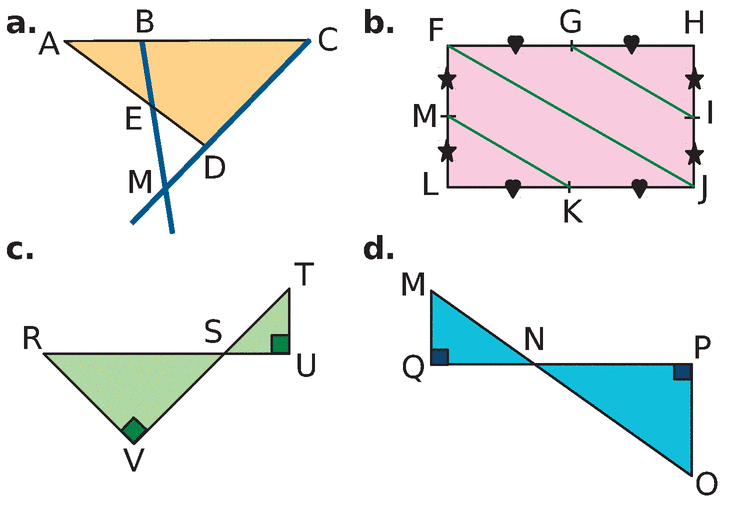
Peux-tu utiliser le théorème de Thalès pour les figures ci-dessous ?
Exercice 2
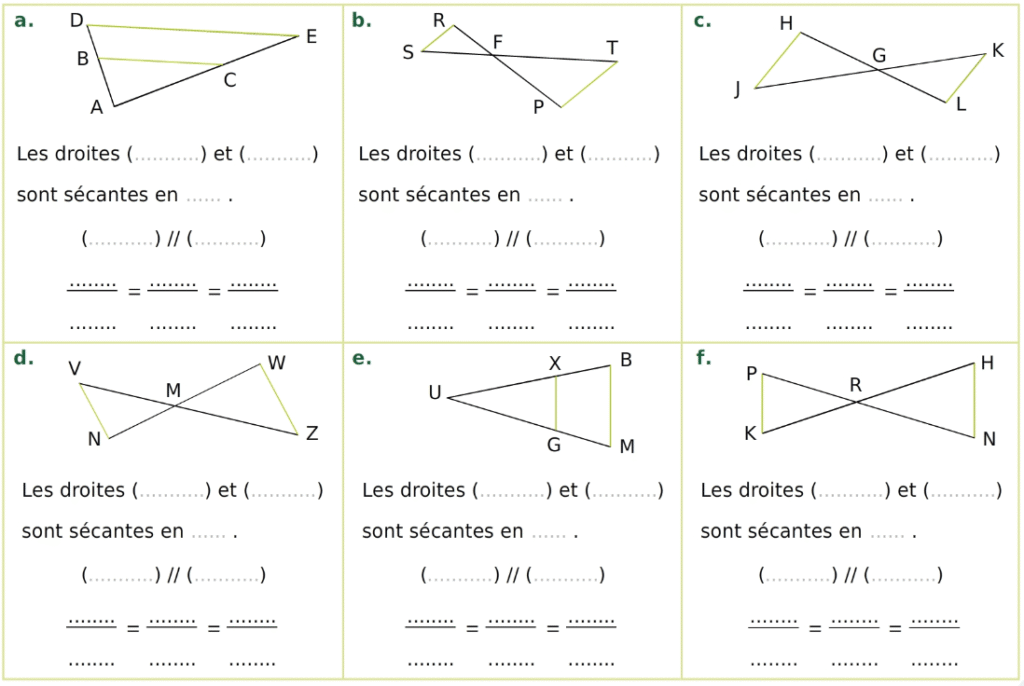
Les droites en vert sont parallèles.
Écris toutes les égalités de rapports de longueurs pour chaque figure.
Exercice 3

Calculer les longueurs EF et IJ
Rédaction
● Les droites (…………) et (…………) sont sécantes en ……
● Les droites (…………) et (…………) sont parallèles
● Donc d’après le théorème de Thalès :
on a : ………… = ………… = …………
soit : ………… = ………… = …………
● d’où EF =
et IJ =
Exercice 4
Calculer les longueurs RT et RA en rédigeant la solution comme dans le modèle ci-dessus.

Exercice 5
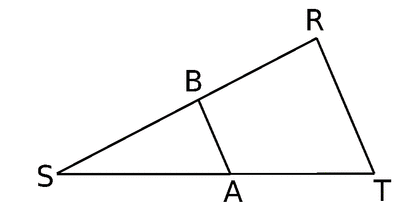
Sur la figure ci-dessous les droites (AB) et (RT) sont parallèles.
On donne SA = 4 cm, ST = 15 cm, AB = 2,4 cm et SR = 7,5 cm
Trace la figue à main levée puis calcule SB et RT.
Exercice 6
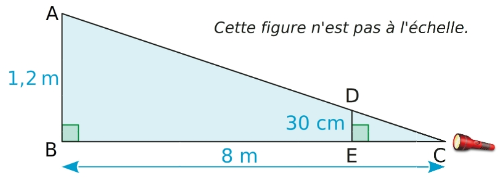
1) Démontre que (AB) et (ED) sont parallèles.
2) Calcule EC.
Exercice 7
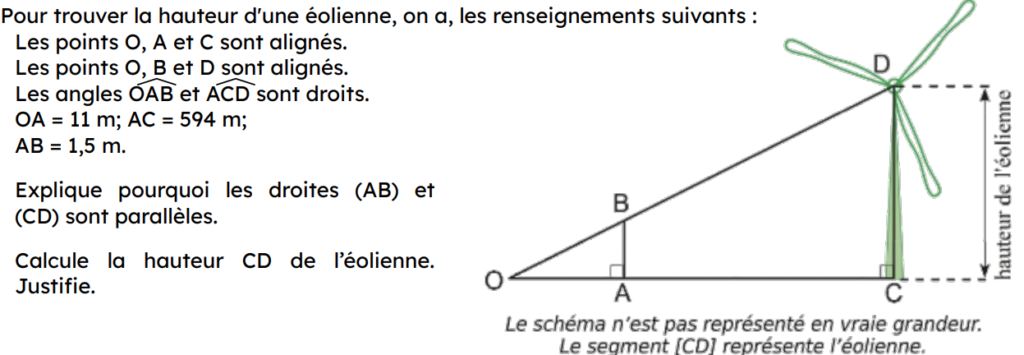
Exercice 8
ABC est un triangle tel que BC = 3,3 cm ; AC = 2,4 cm et AB = 2,5 cm.
a- Réalise une figure. Place le point D sur [CA) tel que CD = 6 cm et le point E sur [CB) tel que CE = 9 cm.
b- Explique pourquoi les droites (ED) et et (AB) ne sont pas parallèles.
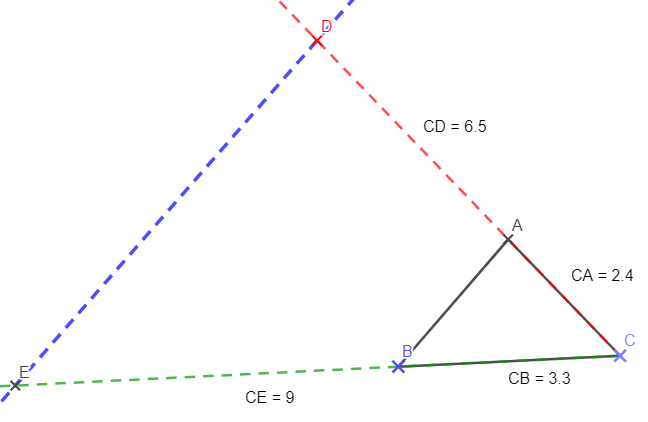
Exercice 9
Les droites (BD) et (CE) sont-elles parallèles ?
On donne les longueurs suivantes :
AB = 6,3 cm ; BC = 4,9 cm ; AE = 16 cm et DE = 7 cm
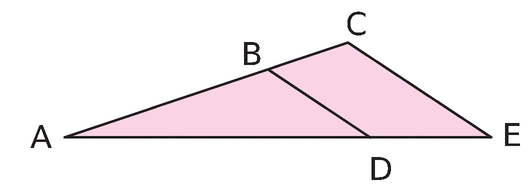
Exercice 10

Affirmation : les droites (AB) et (DC) sont parallèles.
Vrai ou faux ? Justifier.
Exercice 11
Karim a fabriqué une étagère pour y ranger ses livres et ses bandes dessinées. Elle est schématisée ci-dessous:
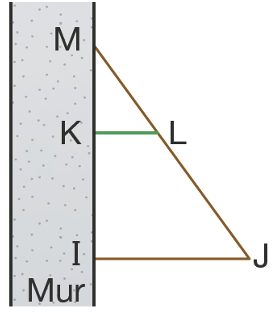
Les triangles MKL et MIJ sont emboîtés.
Karim a effectué les relevés suivants : ML=17 cm ; MJ = 35,7 cm; MK = 14 cm; MI = 29,4 cm.
Démontrer que la planche à livres [KL] est parallèle à la planche à bandes dessinées [IJ].
Exercice 12
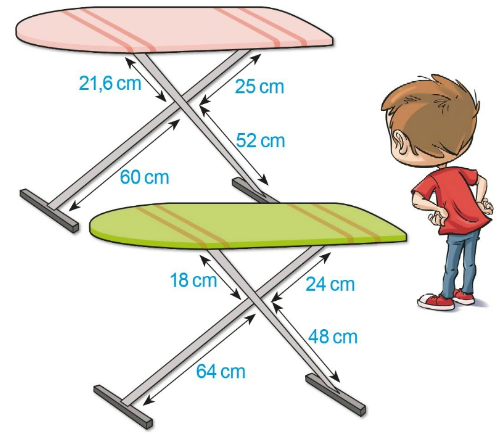
Ces deux tables sont placées sur un plan horizontal, leur plateau est-il horizontal ? Justifie ta réponse.
Exercice 14
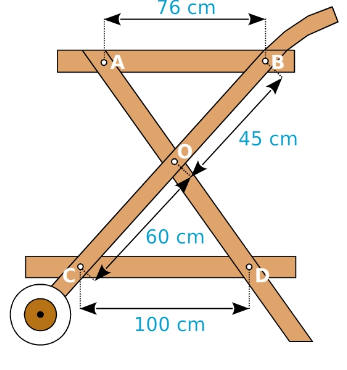
Les plateaux de cette desserte sont-ils parallèles ?
Exercice 15 (extrait d’un sujet de DNB)
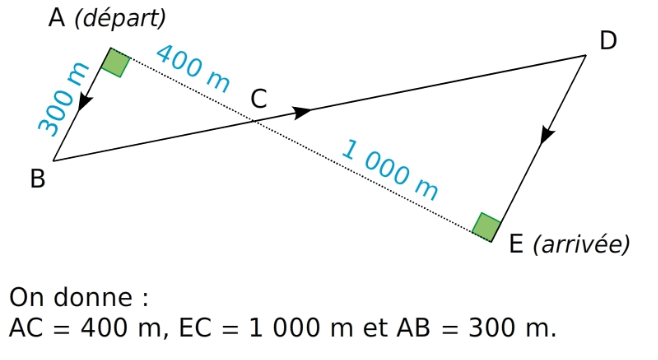
Pour soutenir la lutte contre l’obésité, un collège décide d’organiser une course. Les élèves doivent partir du point A et se rendre au point E en passant par les points B, C et D. (AE) et (BD) se coupent en C.
1) Calcule BC.
2) Montre que ED = 750 m
3) Détermine la longueur réelle du parcours ABCDE.
Exercice 16 (extrait d’un sujet de DNB)
Funiculaire : chemin de fer à traction par câble pour la desserte des voies à très forte pente. (D le point de départ et A le point d’arrivée).
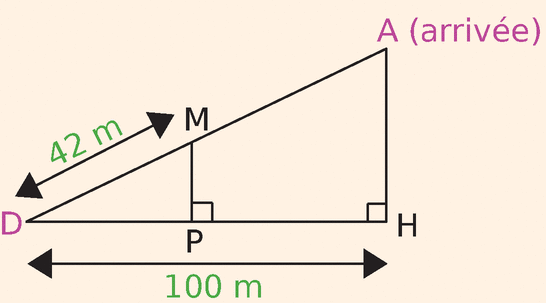
La longueur AD de la voie du funiculaire est de 125 m.
a- De quelle hauteur AH s’est-on élevé à l’arrivée ?
b- Lorsque le funiculaire a parcouru 42 m, il s’est élevé d’une hauteur MP.
- Faire un dessin à l’échelle 1/ 1 000.
- Que peut-on dire des droites (MP) et (AH) ?
- Calculer MP.
Exercice 17 (extrait d’un sujet de DNB)
Le cross du collège : des élèves participent à un cross. Avant l’épreuve, un plan leur a été remis. Il est représenté ci-dessus :
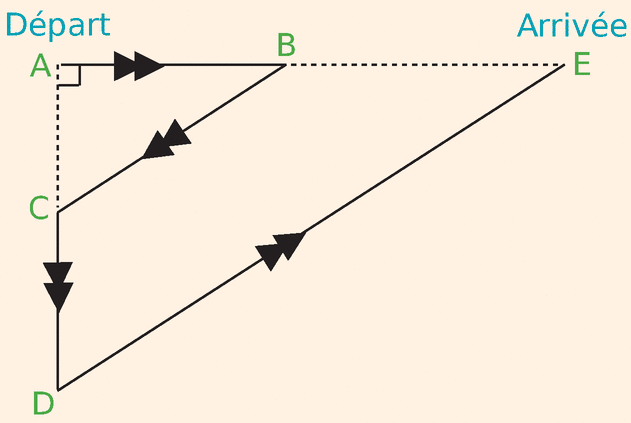
On peut y lire les indications suivantes :
AB = 400 m ; AC = 300 m ; BE = 2AB, les segments [AB] et [AC] sont perpendiculaires et les droites (BC) et (DE) sont parallèles.
- a. Calculer BC.
- b. Calculer AD puis CD.
- c. Calculer DE.
- d. Vérifier que la longueur du parcours ABCDE est de 3 000 m.
Exercice 18
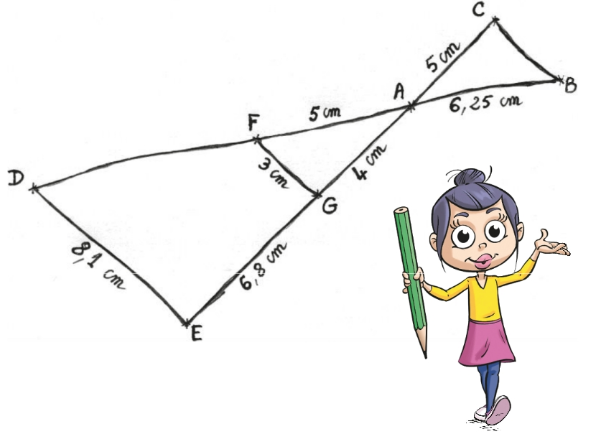

Exercice 19 (extrait d’un sujet de DNB)
Dans les marais salants, le sel récolté est stocké sur une surface plane. On admet qu’un tas de sel a toujours la forme d’un cône de révolution.
1- a. Pascal souhaite déterminer la hauteur d’un cône de sel de diamètre 5 mètres. Il possède une bâton de longueur 1 mètre.
Il effectue des mesures et réalise les deux schémas ci-dessous :
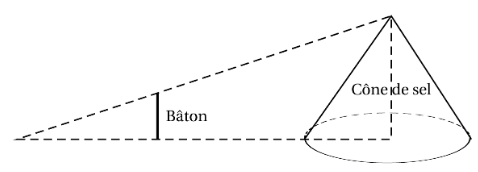
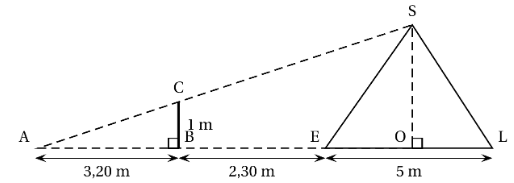
Démontrer que la hauteur de ce cône de sel est égale à 2,50 mètres
1- b. À l’aide de la formule ci-dessous, déterminer en m3 le volume de sel contenu dans ce cône. Arrondir le résultat au m3 près.

2. Le sel est ensuite stocké dans un entrepôt sous la forme de cônes de volumes 1 000 m3 . Par mesure de sécurité, la hauteur d’un tel cône de sel ne doit pas dépasser 6m. Quel rayon faut-il prévoir au minimum pour la base ? Arrondir au décimètre près.