Le théorème de Pythagore
Exercices

Exercice 1
Dire si les affirmations suivantes sont vraies ou fausses. Justifier votre réponse.
a) 49 est le carré de 7.
b) 8 a pour carré 64.
c) -9 a pour carré -81.
d) 144 est le carré de -12.
e) (-3)² est le carré de 3.
Exercice 2
Écrire chaque nombre sous la forme du carré d’un nombre positif.
a) 16
b) 25
c) 0
d) 0,36
e) 1
f) 0,04
Exercice 3
Recopie et complète les phrases suivantes.

Exercice 4
Les nombres suivants ont-ils une racine carrée ?

Exercice 5
Compléter les égalités ci-dessous par des valeurs exactes ou des valeurs approchées arrondies au centième.

Exercice 6
Quand on écrit sur la calculatrice √20, elle renvoie : 4,472135955.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Quand on eˊcrit sur la calculatrice √74, elle renvoie : 8,602325267.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Quand on écrit sur la calculatrice √104, elle renvoie : 10,1980390272.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Exercice 7
Quand on écrit sur la calculatrice 119, elle renvoie : 10,9087121146.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Quand on écrit sur la calculatrice 54, elle renvoie : 7,3484692283.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Quand on écrit sur la calculatrice 255, elle renvoie : 15,9687194227.
Arrondi à l’unité
Arrondi au dixième
Arrondi au centième
Exercice 8
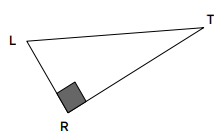
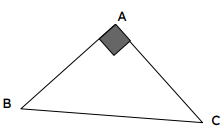
Reproduire sur le cahier le triangle ci-dessous.

1- À quelle condition peut-on utiliser le théorème de Pythagore ?
2- Qu’est-ce que l’hypoténuse ? Repasser en rouge l’hypoténuse.
3- Énoncer le théorème de Pythagore pour le triangle ABC.
Exercice 9
Tracer chaque triangle puis :
❏ repasser l’hypoténuse en rouge
❏ écrire l’égalité de Pythagore

Exercice 10
Exercice 11
Exercice 12
Exercice 13
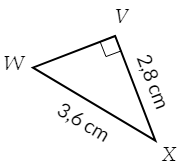
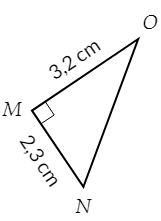
Dans chaque cas, calculer la longueur manquante (si nécessaire, l’arrondir au millimètre près).
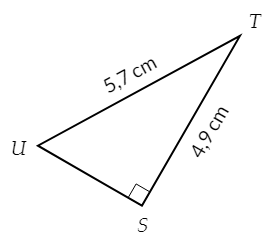
Exercice 14
On considère le triangle QRT rectangle en R tel que :
QT = 10 cm et QR = 5 cm
1- Calculer la valeur exacte de RT.
2- Puis donner une valeur approchée de RT au mm près (soit à 0,1 cm près).
Exercice 15
On considère le triangle ABC rectangle et isocèle en C tel que :
AC = 5 cm
1- Calculer la valeur exacte de AB.
2- Puis donner une valeur approchée de AB au mm près (soit à 0,1 cm près).
Exercice 16
TUVW est un rectangle tel que TU = 4 cm et UV = 4,2 cm.
Calculer TV.
Exercice 17
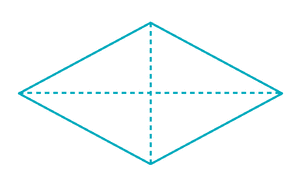
ABCD est un losange de centre O tel que AC = 6 cm et BD = 8 cm
a- Tracer la figure à main levée et place les sommets.
b- Calculer AB puis le périmètre de ce losange.
Exercice 18
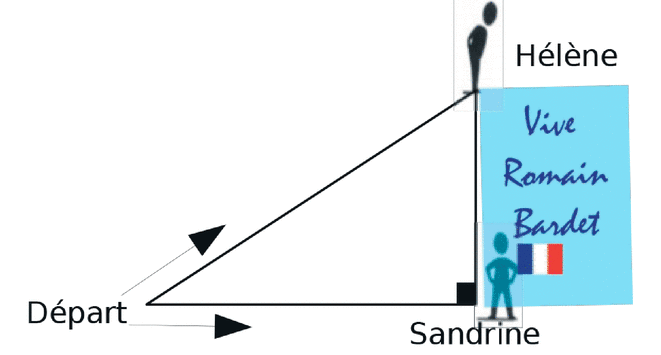
Hélène et Sandrine ont décidé d’aller sur les routes du Tour de France cycliste pour encourager leur sportif préféré, Romain Bardet. Elles ont prévu une grande banderole de 4 m de haut.
Hélène est montée sur une estrade et déroule la banderole. Sandrine, restée sur le plat, a rejoint le pied de la banderole à 10 m.
Quelle distance, arrondie au mètre, Hélène a-t-elle parcourue ?
Exercice 19
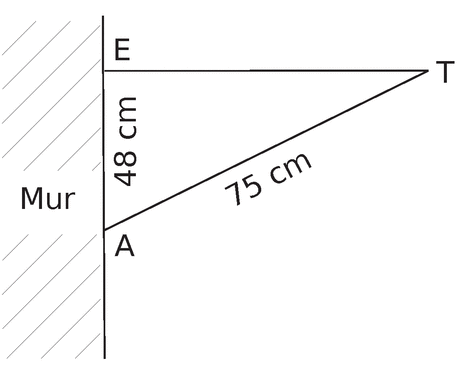
Karim a posé une étagère dans sa chambre sur un des murs. On suppose que ce mur est perpendiculaire au sol et que l’étagère est parallèle au sol.
Déterminer une valeur approchée au millimètre près de la largeur de l’étagère.
Exercice 20
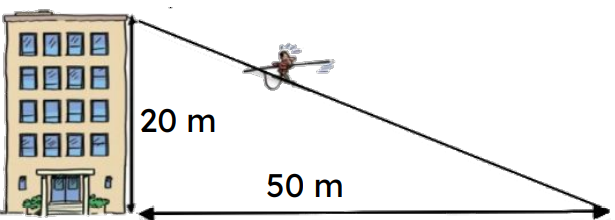
Un cascadeur descend de cet immeuble accroché à un câble.
Quelle distance va-t-il parcourir sur le câble ?
Exercice 21
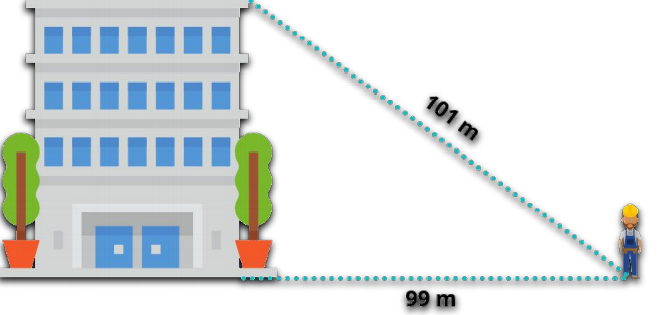
Ton collègue jure connaître la hauteur d’un immeuble sans l’avoir mesurée de bas en haut avec un
télémètre. Selon les données que tu vois sur son positionnement, a-t-il raison d’affirmer que l’immeuble
mesure 20 m de haut ?
ÉCRIS ton raisonnement et tes calculs.
Exercice 22 (extrait d’un DNB)
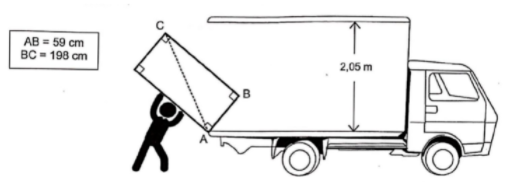
Lors de son déménagement, Allan doit transporter son réfrigérateur dans un camion. Pour l’introduire dans le camion, Allan le pose sur le bord comme indiqué sur la figure.
Le schéma n’est pas à l’échelle.
Allan pourra-t-il redresser le réfrigérateur en position verticale pour le rentrer dans le camion sans bouger le point d’appui A ? Justifier.
Exercice 23 (extrait d’un DNB)
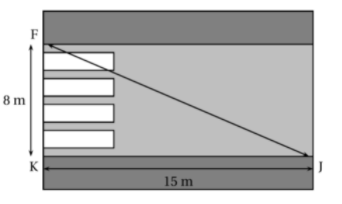
Julien est en retard pour aller rejoindre ses amis au terrain de basket. Il décide alors de traverser imprudemment la route du point J au point F sans utiliser les passages piétons.
Le passage piéton est supposé perpendiculaire au trottoir.
En moyenne, un piéton met 9 secondes pour parcourir 10 m. Combien de temps Julien a-t-il gagné en traversant sans utiliser le passage piéton ?
Exercice 24 (extrait d’un DNB)
On dispose des informations suivantes : Toutes les valeurs présentes sur les schémas sont en cm. Le fusil sous-marin peut-il être placé “à plat” dans la remorque ? Justifier.
