Égalité de triangles
Définition 1
Deux triangles sont superposables lorsqu’on peut les faire coïncider par glissement et/ou retournement.
Des triangles égaux sont des triangles superposables, c’est-à-dire qui ont des côtés deux à deux de même longueur (et des angles deux à deux de même mesure).
Exemple 0
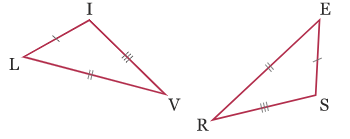
D’après la figure, LI=SE, LV=RE et IV=RS donc les triangles ILV et RSE sont égaux.
Définition 2
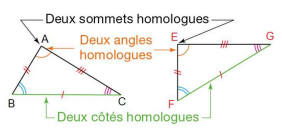
Les triangles ABC et EFG sont donc égaux.
Lorsque deux triangles sont égaux :
– les deux angles superposables sont dits homologues ainsi que leurs sommets.
– les deux côtés superposables sont dits homologues.
Propriété 1
Si deux triangles ont leurs côtés deux à deux de même longueur, alors ils sont égaux.
Exemple 1

Propriété 2
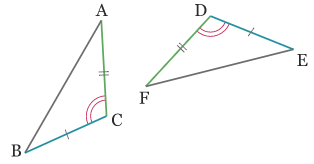
Si deux triangles ont un angle de même mesure compris entre deux côtés deux à deux de même longueur, alors ces deux triangles sont égaux.
Exemple 2
Propriété 3
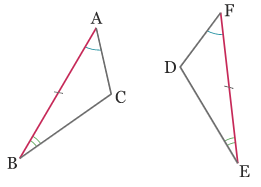
Si deux triangles ont un côté de même longueur compris entre deux angles deux à deux de même mesure, alors ces deux triangles sont égaux.
Exemple 4
Méthode
- On cherche s’il y a des données en commun entre les deux triangles : longueurs des côtés et/ou angles de même mesure.
- On identifie et cite la propriété correspondante.
- On conclut.
Exemples de rédactions attendues
Exercice 1
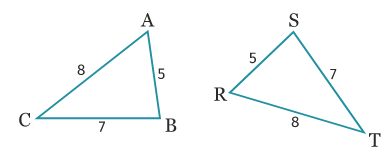
On a AC = RT ; CB = ST ; AB = SR donc les triangles ABC et RST sont égaux car d’après la propriété n°1, on sait que si deux triangles ont leurs côtés deux à deux de même longueur alors ils sont égaux.
Exercice 2
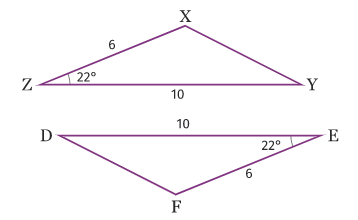
Les triangles ZXY et DFE sont égaux car d’après la propriété n°2, si deux triangles ont un angle de même mesure compris entre deux côtés deux à deux de même longueur, alors ces deux triangles sont égaux.
Exercice 3
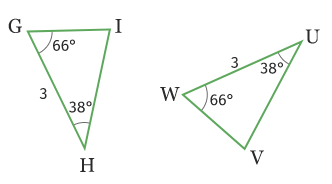
Les triangles GHI et VWU sont égaux car d’après la propriété n°3, Si deux triangles ont un côté de même longueur compris entre deux angles deux à deux de même mesure, alors ces deux triangles sont égaux.