Transformations géométriques
Exercices

Exercice 0
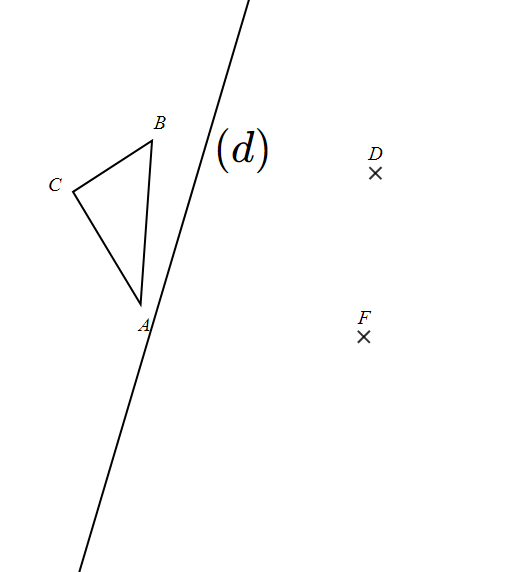
Construire à partir de la figure ci-dessous :
Construire
A1B1C1 le triangle symétrique de ABC par rapport à la droite (d).
A2B2C2 le triangle symétrique de A1B1C1 par rapport au point D.
A3B3C3 le triangle translaté de A2B2C2 par la translation qui transforme D en F.
A4B4C4 le triangle obtenu par la rotation de A3B3C3 de centre F et d’angle 97° dans le sens des aiguilles d’une montre.
série d’exercices sur la translation
série d’exercices sur la rotation
Exercice 1
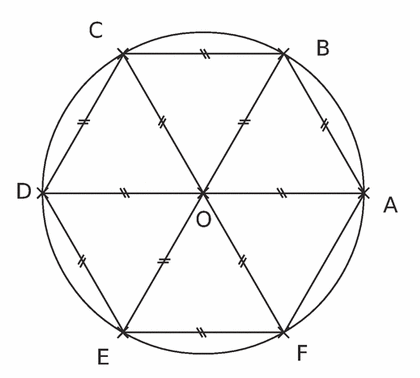
1) On considère la rotation de centre O et d’angle 60° dans le sens inverse des aiguilles d’une montre.
Quelle est l’image du point A ? ……………….
du point F ? ………………..
du triangle OBA ? …………………
du losange ODEF ? ………………….
2) On considère la rotation de centre C et d’angle 60° dans le sens des aiguilles d’une montre.
Quelle est l’image du point B ? ……………….
du point A ? ………………..
du triangle OBA ? …………………
du losange OABC ? ………………….
3) On considère les rotations de centre O. Détermine les caractéristiques de la rotation permettant d’affirmer que :
E est l’image du point A ? ………………………………………………………………………..….
F est l’image du point E ? ………………………………………………………………………..….
A est l’image du point D ? ………………………………………………………………………..….
E est l’image du point F ? ………………………………………………………………………..….
4) Placer le point G, image du point B par la rotation de centre A, d’angle 60° dans le sens des aiguilles d’une montre.
5) Tracer l’image du losange ODEF par la rotation de centre F, d’angle 120° dans le sens des aiguilles d’une montre.
6) Placer le point H, image du point B par la rotation de centre O, d’angle 30° dans le sens inverse des aiguilles d’une montre.
7) Placer le point I, image du point C par la rotation de centre O, d’angle 150° dans le sens inverse des aiguilles d’une montre.
Exercice 2
Dans cet exercice, toutes les rotations sont d’angle 90°.

a) L’image du segment [BL] par la rotation de centre P dans le sens des aiguilles d’une montre est le segment ……
b) L’image du triangle GIM par la rotation de centre M dans le sens inverse des aiguilles d’un montre est le triangle …………
c) Le segment [AM] est l’image du segment [ME] par la
rotation de centre …….. dans le sens……………………………………………………………………………………..
d) Le parallélogramme ACIG a pour image le parallélogramme GQUK par la rotation de centre …… dans le sens des aiguilles d’une montre.
e) Représenter en rouge l’image du parallélogramme ACIG par la rotation de centre M dans le sens des aiguilles d’une montre.
Exercice 3
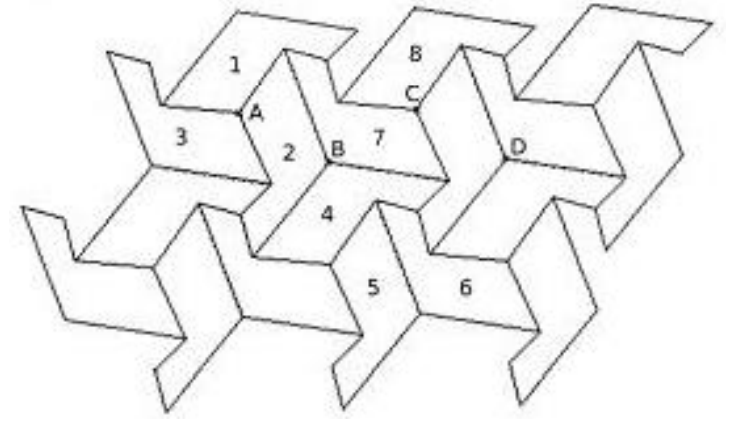
Donner le centre, l’angle et le sens de la rotation qui transforme 1 en 2 :
…………………………………………………………………………………………
Celle qui transforme 2 en 4 :
…………………………………………………………………………………………
Quelle est l’image du motif 2 par la rotation de centre B d’angle 120° dans le sens inverse des aiguilles d’une montre ? …………………………………………………
Quelle est l’image du motif 1 par la rotation de centre C d’angle 120° dans le sens inverse des aiguilles d’une montre ? …………………………………………………
Quelle est l’image du motif 6 par la rotation de centre D d’angle 120° dans le sens des aiguilles d’une montre ? …………………………………………………
Quelle rotation permet de passer du motif 5 au motif 8 ? (donner le centre, l’angle et le sens)
………………………………………………………………………………………………………………
Exercice 4

Dans cet exercice toutes les rotations sont de centre A.
H : sens horaire (sens des aiguilles d’une montre)
AH : sens anti-horaire (sens inverse des aiguilles d’une montre)
Compléter le tableau suivant :

Exercice 5
ABCO, CDEO, EFGO et GHAO sont des carrés. BDFH est un carré de centre O.
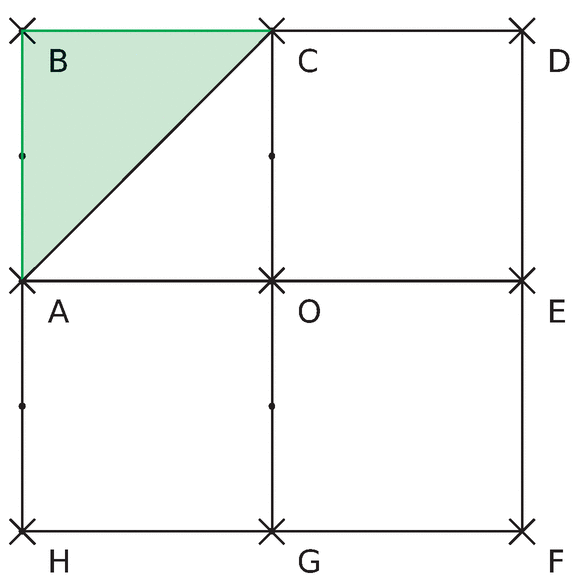
Quelle est l’image du triangle ABC dans les cas suivants ?
(On donnera ces résultats sans les justifier.)
1- Par la rotation de centre O, d’angle 90°, qui amène G en E.
2- Par la translation qui transforme B en O.
3- Par la symétrie d’axe (AE).
4- Par la symétrie centrale de centre O.
Exercice 6
Reproduire sur le cahier la figure ci-dessous qui représente des triangles équilatéraux.

1-Construire le point Q, symétrique de A par rapport à la droite (BE).
2- Construire le point P, image du point J par la rotation de centre I et d’angle 120° dans le sens inverse des aiguilles d’une montre.
3- Quelle transformation permet de passer du triangle ABC au triangle IRF ? Préciser ses éléments caractéristiques.
4- Quelle transformation permet de passer du triangle ABD au triangle RIF ? Préciser ses éléments caractéristiques.