Calculer le volume d’un solide-3
La sphère et la boule
1- Définition de la sphère
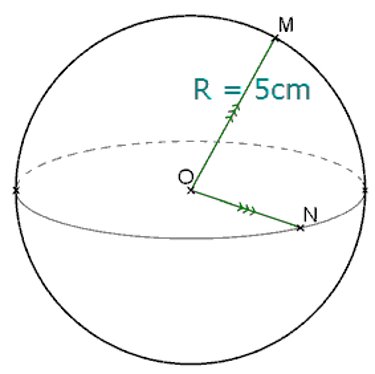
Dans l’espace, une sphère de centre O et de rayon R est l’ensemble des points M, tels que OM = R
Ce sont des objets creux, vides comme un ballon ou une balle de Ping-Pong.
2- Aire de la sphère
L’aire d’une sphère de rayon R est A = 4πR²
Exemple
Calcule l’aire d’une sphère de rayon 5 cm.
A = 4πR²
A = 4×π×5²
A ≈ 4×3,14×25
A ≈ 314 cm²
Exercices d’application
1- Calcule l’aire de la sphère ci-dessous.

2- Calcule l’aire d’une sphère de diamètre 12,6 cm
3- Quel est le diamètre d’une sphère d’aire 36𝜋 cm2 ?
4- Détermine le rayon de la sphère dont l’aire est 50 cm2.Arrondis ta réponse au centième près.
5- Détermine l’aire totale de l’hémisphère. Arrondis la réponse au dixième.

3- Définition de la boule
Dans l’espace, une boule de centre O et de rayon R est l’ensemble des points M’, tels OM’≤R
Ce sont des objets pleins comme une boule de pétanque, la planète Terre...
4- Volume de la boule
Le volume d’une boule de rayon R est :
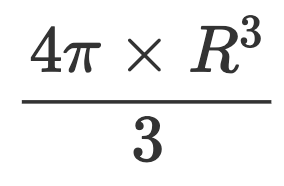
Exemple :
Calcule le volume d’une boule de rayon 2 cm.

V =
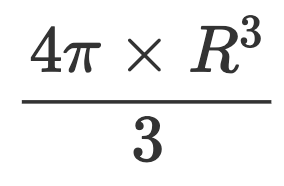
V ≈ 32×3,14/3
V ≈ 32×3,14/3
V ≈ 33,49 cm3
Exercices d’application
1- La Terre peut être considéré comme une boule de rayon moyen de 6 371 km.
Calcule son volume.

2-Calcule le volume de la boule ci-dessous.

3-Calcule le volume de cette demi-boule.

4- Calcule le volume de cette boule sachant qu’elle est complètement immergée dans un cube de volume égal à 8 cm3.

5- Calcule le volume de cette boule sachant qu’elle est complètement immergée dans un cylindre de volume 16𝜋 cm3. La hauteur du cylindre est égale au diamètre de la boule.

Exercice corrigé : aire et volume d’une boule
Exercice corrigé : volume d’une boule et d’un cône
Exercice corrigé : volume d’une boule et d’un cylindre