Calcul littéral : double distributivité, identités remarquables
Exercices

Exercice 1
Somme ou produit ?
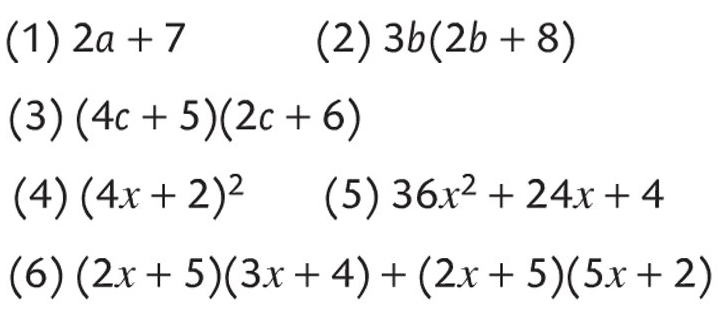
Exercice 2
Somme ou produit ?

Exercice 3
Reduire si possible.
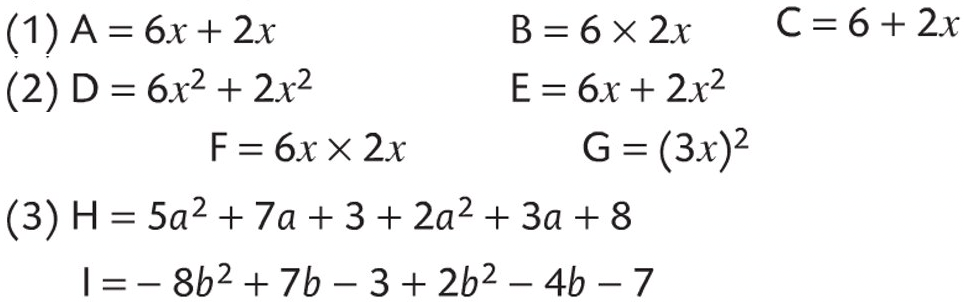
Exercice 4
Reduire si possible.
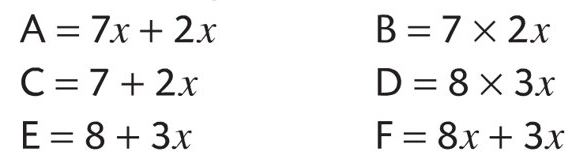
Exercice 5
Réduire si possible.
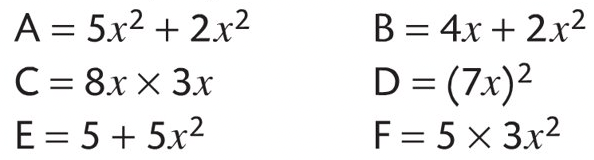
Exercice 6
Développer et réduire si possible.
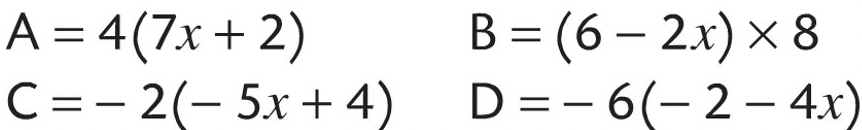
Exercice 7
Développer et réduire si possible.
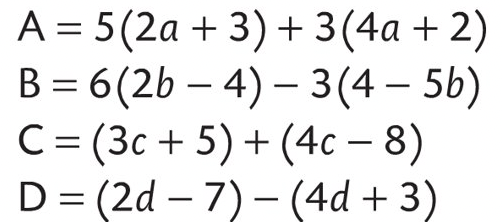
Exercice 8
Développer et réduire si possible.
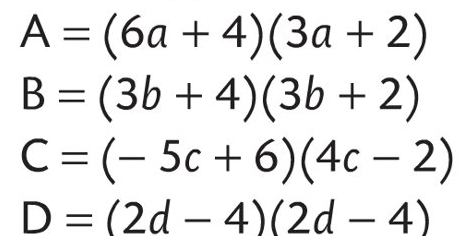
Exercice 9
Développer et réduire si possible.

Exercice 10
Développer et réduire si possible.
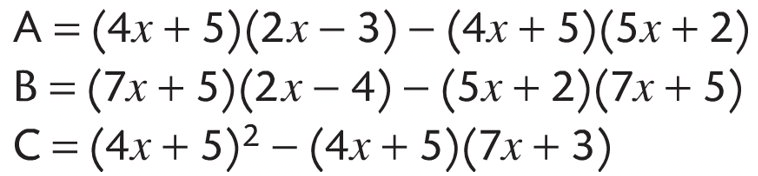
Exercice 11
Exercice extrait d’un brevet.
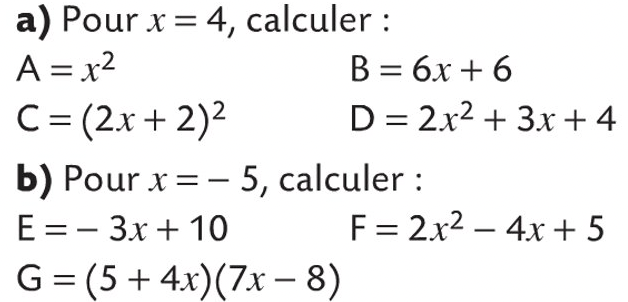
Exercice 12
- On considère les programmes de calcul suivants :
Programme A :
– choisir un nombre,
– le doubler,
– puis enlever 7.
Programme B :
– choisir un nombre,
– lui soustraire 4,
– multiplier le résultat par 2,
– ajouter 1.
1) Tester ces programmes avec le nombre 4 et en choisissant un autre nombre quelconque. Émettre une conjecture.
2) Prouver cette conjecture.
Exercice 13
- On considère les programmes de calcul suivants :
Programme A :
– choisir un nombre,
– le multiplier par 6,
– puis enlever 15.
Programme B :
– choisir un nombre,
– lui soustraire 2,
– multiplier le résultat par 6,
– soustraire 3.
1) Tester ces programmes avec le nombre 2 et en choisissant un autre nombre quelconque. Émettre une conjecture.
2) Prouver cette conjecture.
Exercice 14
Clara a renregsitré trois émissions sur un DVD.
La première dure 𝑥 minutes. La deuxième 10 minutes de plus que la première et la troisième le double de la deuxième.
a) Ecrire en fonction de 𝑥 la durée de chaque émission.
b) Ecrire en fonction de 𝑥 la durée totale de l’enregistrement.
c) Si la première émission dure 15 min, quelle est la durée totale de l’enregistrement ?
Exercice 15
Un stade comporte 15 000 places.
Il y a 𝑥 places dans les virages et les autres dans les tribunes. Une place en virage coûte 25 € et une place dans les tribunes 35 €.
Aujourd’hui, le stade est plein.
a) Ecrire, en fonction de 𝑥, la recette du match. Présenter le résultat sous forme d’une expression développée et réduite.
b) Il y a 7 000 places dans les tribunes, quelle est la recette ?
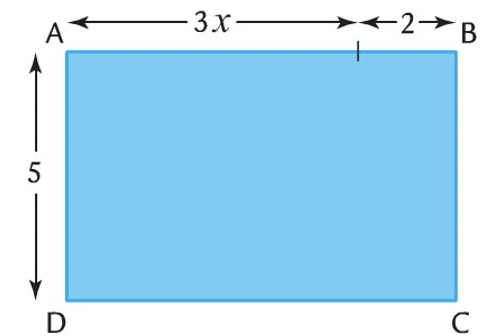
Exercice 16
Ecrire le périmètre puis l’aire du rectangle ABCD en fonction de 𝑥.
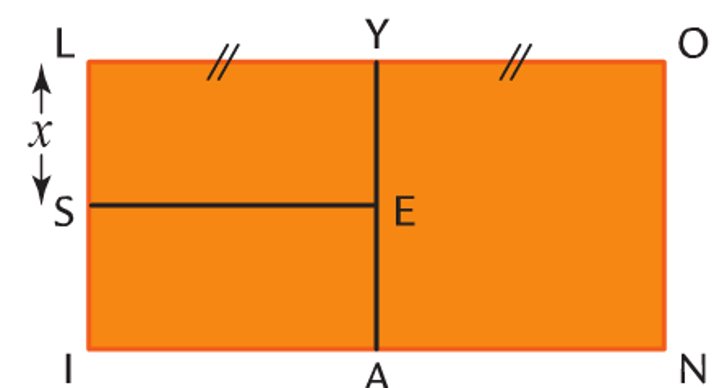
Exercice 17
La figure ci-dessous est formée de rectangles LYES et SEAI identiques et d’un carré YONA.
a) Ecrire la longueur LO en fonction de 𝑥.
b) Ecrire le périmètre de LONI en fonction de 𝑥.
c) Ecrire l’aire de LONI en fonction de 𝑥.
Exercice 18
Développer avec les identités remarquables.

Exercice 19
Développer avec les identités remarquables.

Exercice 20
Développer avec les identités remarquables.

Exercice 21
Développer avec les identités remarquables.

Exercice 22

Exercice 23

Exercice 24
𝑥 est un nombre positif, montrer que le triangle PAS est un triangle rectangle.