Définition

• Factoriser, c’est transformer une somme (ou une différence) en un produit.​

• Développer, c’est transformer un produit en une somme (ou en une différence.)​

• Réduire, c’est effectuer tous les calculs possibles et appliquer les conventions d’écriture.​

• Une expression est une somme si la dernière opération à effectuer est une addition.​

• Une expression est une différence si la dernière opération à effectuer est une soustraction.​

• Une expression est un produit si la dernière opération à effectuer est une multiplication.

Propriété : développer une expression à l’aide de la simple distributivité

k, a et b désignent des nombres.

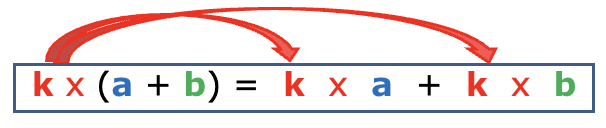
Exemple 1

13 X (13 + a) = 13 X 13 + 13 X a = 169 + 13a

Exemple 2

13 X (13 – a) = 13 X 13 – 13 X a = 169 – 13a

Propriété : développer une expression à l’aide de la double distributivité

a, b, c et d désignent des nombres.

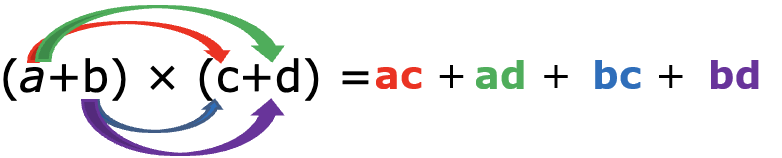
Exemple 1

(3a +4)(b + 10) = 3a x b + 3a x 10 + 4 x b + 4 x 10

​= 3ab + 30a + 4b + 40

Exemple 2

(3a + 4) (2b – 3) = 3a x 2b + 3a x (-3) + 4 x 2b + 4 x (-3)

= 6ab – 9a + 8b – 12

Exemple 3

(5a – 9) (2a – 3) = 5a x 2a + 5a x (-3) +(-9) x 2a + (-9) x (-3)

= 10 a² – 15a -18a + 27 = 10 a² – 33a + 27

 Calcul littéral : développer une expression-1

 Calcul littéral : développer une expression-2

 Calcul littéral : développer une expression-3

 Calcul littéral : développer une expression-4

Activité

Développer les expressions suivantes

(a + b)² = (a + b) (a + b) =

(a – b)² = (a – b) (a – b) =

(a + b) (a – b) =

• Identités remarquables (développement)

 Identités remarquables #1

 Identités remarquables #2

Pages : 1 2 3