Calcul littéral
Activité 1 : Les maisons
Chaque figure est constituée d’un triangle équilatéral ABC et d’un carré DEFG.
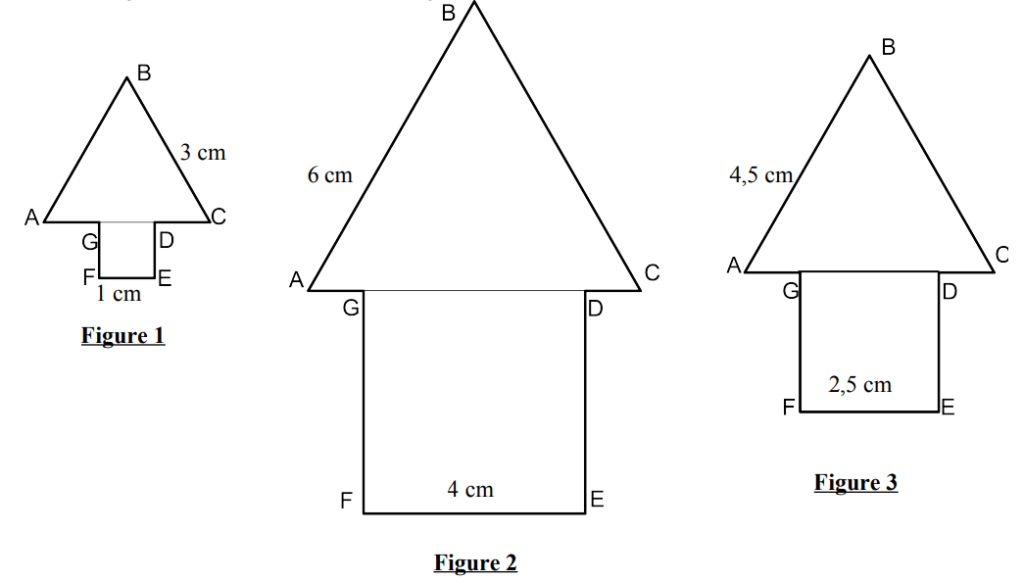
1- Dessiner une quatrième figure sur le même modèle.
2- Déterminer le périmètre de chacune des trois figures données.
3- Écrire un programme de calcul du périmètre de la figure à partir de la longueur du côté du
carré.
4- Traduire ce programme par une formule utilisant les signes +, -, ×, des parenthèses, des
nombres, des lettres mais pas de mots.
5- Vérifier cette formule pour les trois figures.
6- On veut construire une cinquième figure dont le périmètre est 41 cm. Quelle longueur doit-on choisir comme côté du carré ?
1) Définition :
Une expression littérale est une expression mathématique qui contient une ou plusieurs lettres. Ces lettres désignent des nombres.
Exemples :
L’aire d’un carré de côté c : Aire = c × c
Le périmètre d’un carré de côté c : Périmètre = 4 × c
On le dit que l’aire et le périmètre sont des expressions littérales.
2) Simplification d’une expression littérale
On peut simplifier les expressions littérales en supprimant le signe de multiplication (×) lorsqu’il est suivi d’une lettre ou d’une parenthèse.
Exemples :
(2 × a) devient (2a)
2 × ( L + l ) = 2 ( L + l )
1 × a = a
o × a = 0
a × a = a² , on lit a au carré
a × a × a = a³ , on lit a au cube
Aire = c × c = c²
3) Évaluer une expression littérale
Pour évaluer (calculer) une expression littérale, on remplace les lettres par des valeurs numériques.
Exemples :
Le périmètre d’un carré de côté c : Périmètre = 4 × c si c = 6 cm alors Périmètre = 4 × c = 4 × 6 = 24 cm
Le périmètre d’un rectangle de longueur 8 cm et de largeur 5 cm :
Périmètre = = 2 ( L + l ) = 2 ( 8 + 5 ) = 2 ×13 = 26 cm
si A = 5(𝒙 + 2)) et (𝒙 = 3), alors (A = 5 × (3 + 2) = 25).
4) Tester une égalité
Une égalité est constituée de deux membres séparés par le signe (=).
On peut tester une égalité en remplaçant chaque lettre par sa valeur dans chaque membre.
On compare ensuite les résultats :
- S’ils sont égaux, on dit alors que l’égalité est vraie
- S’ils sont différents, on dit alors que l’égalité est fausse
Exemples :
4𝒙 + 2 = 2𝒙 + 4
Testons cette égalité pour 𝒙 = 0
4 × 0 + 2 = 2 et 2 × 0 + 4 = 4 et comme 2 ≠ 4 donc cette égalité est fausse pour 𝒙 = 0
Testons cette égalité pour 𝒙 = 1
4 × 1 + 2 = 6 et 2 × 1 + 4 = 6 et comme 2 = 4 donc cette égalité est vraie pour 𝒙 = 0
5) Produire une expression littérale
Soit n un entier quelconque :
Le double de n est 2 × n = 2n
Le triple de n est 3 × n = 3n
Le carré de n est n × n = n²
L’entier consécutif à n est n + 1
L’entier précédant n est n – 1
Exemple :
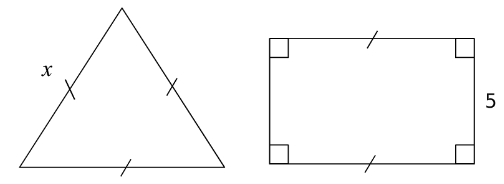
Exprimer en fonction de 𝒙 le périmètre de chaque figure.