Arithmétique (Partie 1)

I-Déterminer les diviseurs d’un nombre entier
Fiche 1 (Leçon) : Division euclidienne
1-Déterminer les diviseurs d’un nombre entier
a) Définition :
Un entier naturel est un nombre entier positif ou nul : {0; 1; 2; 3; …}
b) Vocabulaire :
Une division est un partage équitable d’un ensemble d’objets.
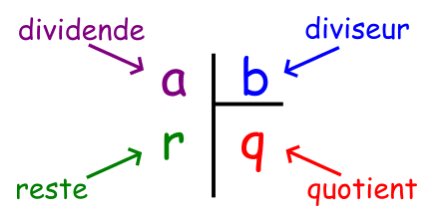
Le nombre que l’on divise s’appelle dividende.
Le nombre par lequel on divise s’appelle le diviseur.
Le résultat s’appelle quotient.
Exemples :
Exemple 1
On partage 96 bonbons entre 20 élèves.
Combien chaque élève aura-t-il de bonbons ?
Réponse : Chaque élève reçoit 4 bonbons et il reste : 16 bonbons.
Exemple 2
Avec 96 bonbons, combien de sachets de 20 bonbons peut-on faire ?
Réponse : On peut faire 4 sachets de 20 bonbons et il reste : 16 bonbons.
Exemple 3
On partage 96 € entre 20 élèves.
Quelle somme chaque élève touchera-t-il ?
Réponse : Chaque élève recevra : 4,80 €.
c) Division euclidienne :
Lorsque dividende, diviseur, quotient et reste sont entiers, on parle de division euclidienne.
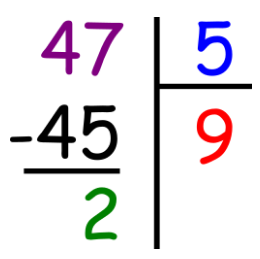
47 = 5 × 9 + 2
Effectuer la division euclidienne de 47 par 5, c’est déterminer le quotient q et le reste r tel que : 47 = 5 x q + r avec r < 3
Le reste est toujours plus petit que le diviseur.
Le diviseur est toujours différent de zéro car on ne peut jamais diviser par 0 !
Plus généralement si a et b désignent deux entiers naturels (b≠0),
Effectuer la division euclidienne de a par b, c’est déterminer le quotient q et le reste r tel que : a = b x q + r avec r < b
Exercice d’application
- Effectue la division euclidienne de 183 par 12.
- 278 = 6 × 45 + 8 : quelle(s) division(s) euclidienne(s) cette égalité
représente-t-elle ?
Correction
On peut donc écrire :
183 = 12 × 15 + 3
avec 3 < 12.
8 < 45 mais 8 > 6 donc l’égalité représente la division euclidienne de 278 par 45 mais ne peut pas représenter celle de 278 par 6.
Activité : « LE PROBLÈME DU CENTURION »

Le centurion ordonne à ses légionnaires :
« Rangez-vous par 4 ! ». Les soldats s’exécutent, mais le dernier rang est incomplet : il ne compte que 3 soldats.
« Mettez-vous par 5 ! », hurle alors le centurion ; mais au dernier rang, incomplet, on compte de nouveau 3 soldats.
« Eh bien, rangez-vous par 7 ! ». Encore une fois, le dernier rang reste
incomplet : on y compte toujours 3 soldats.


Fiche d’exercices n°1
Exercices : source : (Sésamath Cycle 4 Edition 2016)
Exercice n°2 p 74
Écris la division euclidienne correspondant à chacune de ces phrases.
a. Le quotient de 745 par 7 est 106 et le reste est 3.
b. Le dividende est 78, le diviseur est 9, le quotient 8 et le reste 6.
Exercice n°3 p 74
On donne les égalités : 415 = 7 × 59 + 2 et 56 × 57 = 3 192.
Sans effectuer de calculs, donne le quotient et le reste des divisions euclidiennes suivantes.
a. 415 par 7
b. 415 par 59
c. 3 192 par 56
d. 3 192 par 57
Exercice n°5 p 74
Posée, puis en ligne
a. Donne le quotient et le reste de la division euclidienne de :
63 par 4 ;
218 par 12 ;
3 245 par 135 ;
32 par 50.
b. Dans chaque cas, écris l’égalité a = bq + r, où q et r sont des entiers naturels et r < b.
Exercice n°6 p 74
À la recherche du reste
Dans la division euclidienne de 2 654 par 12, le quotient est 221. Sans effectuer la division, détermine le reste.
