Les solides : pyramide et cône de révolution

I- La pyramide

II- Le cône de révolution

1- Définition du cône de révolution

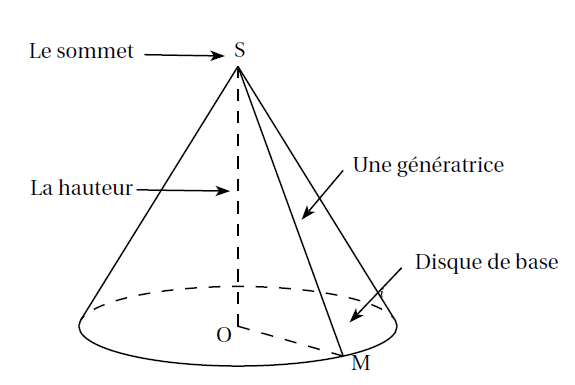
Un cône de révolution est un solide obtenu par rotation d’un triangle rectangle autour d’un axe correspondant à l’un des côtés formant l’angle droit.
Il est constitué d’une base qui correspond à un disque et d’une surface latérale conique.
Le cône possède, comme la pyramide, une hauteur qui correspond à la droite perpendiculaire à sa base et passant par son sommet.

2- Volume d’un cône de révolution

Le volume d’un cône de révolution de rayon R et de hauteur h est donné par la formule suivante :

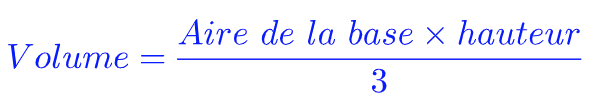
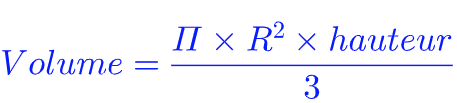
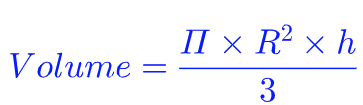
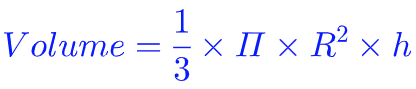
Exemple

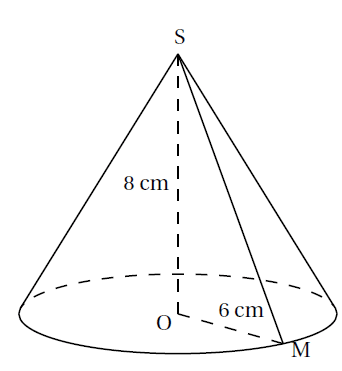
Calculer le volume, en cm³, le volume d’un cône de hauteur 8 cm et de rayon de base 6 cm. Donner une valeur approchée à l’unité près.

Réponse

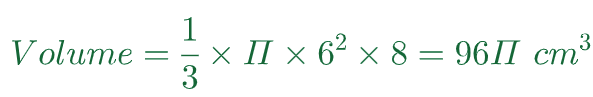
3- Patron d’un cône de révolution

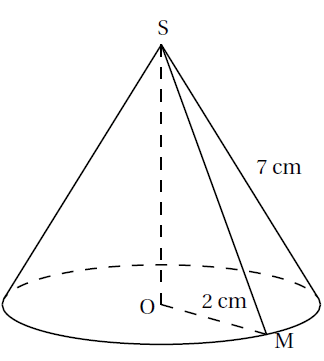
On souhaite construire le patron du cône ci-dessous :

On commence par tracer un patron à main levée.

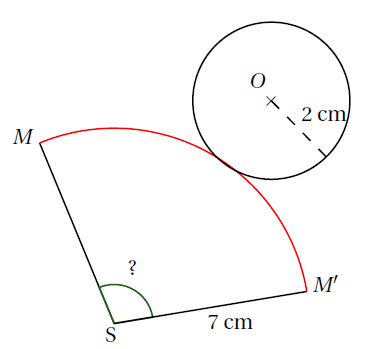
On obtient un disque de rayon 2 cm et une partie d’un disque de rayon SM = 7 cm. Cela revient à déterminer la mesure de l’angle MŜM’.

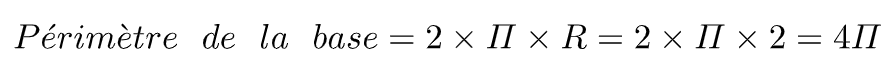
Or, le périmètre de la base est égal à la longueur de l’arc MM’ pour bien fermer le solide, don on a :

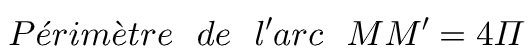
On également, le périmètre du disque de centre S et de rayon 7 cm.

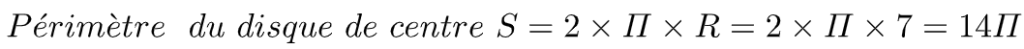
Dans un cercle, la longueur de l’arc est proportionnelle à la mesure de l’angle au centre qui le définit.

Ainsi, pour calculer la mesure de l’angle 𝑀Ŝ𝑀’, on utilise un tableau de proportionnalité :

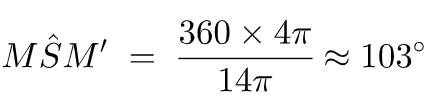
Activité :

Une classe de 4ème compte 24 élèves. Leur enseignant souhaite leur
faire construire des saupoudreurs et les remplir de poudre de stevia, un
édulcorant naturel sans calorie.
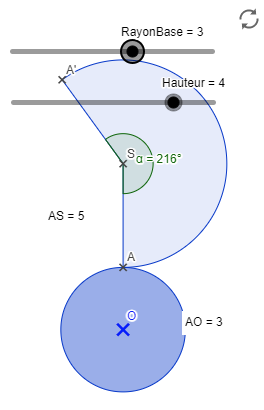
Les saupoudreurs sont constitués d’un cylindre surmonté d’un cône. Les
dimensions sont indiquées sur la figure ci-dessous.

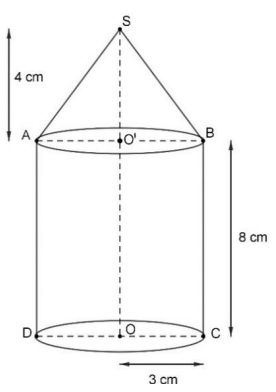
1. Déterminer le volume exact du cône en cm³.

2. Déterminer le volume exact du cylindre en cm³.

3. Démontrer que la génératrice [SA] du cône mesure 5 cm.

4. Quelle quantité de stevia est nécessaire pour l’ensemble de la
classe ? Arrondir le résultat au litre.

6. Afin de réaliser un patron de cône, l’enseignant dessine le croquis ci-dessous (croquis 1) où 𝛼 est l’angle au centre du cercle de centre S et de rayon 5 cm qui intercepte l’arc d’extrémités A et A′.

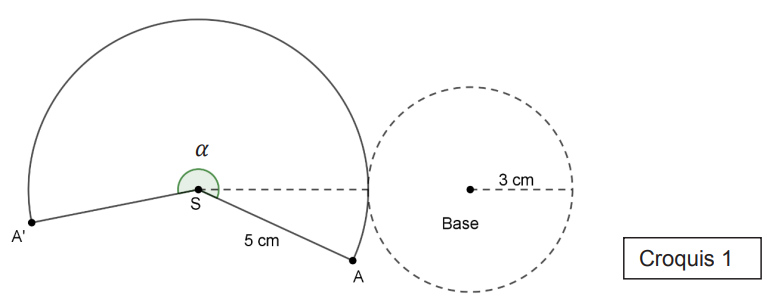
a. Déterminer la longueur de l’arc de cercle d’extrémités A et A′. Justifier la réponse.
b. En déduire la mesure de l’angle 𝛼 au degré près.
On rappelle que la longueur de l’arc de cercle d’extrémités A et A’ est proportionnelle à l’angle au centre 𝛼 et on pourra s’aider du tableau ci-dessous :

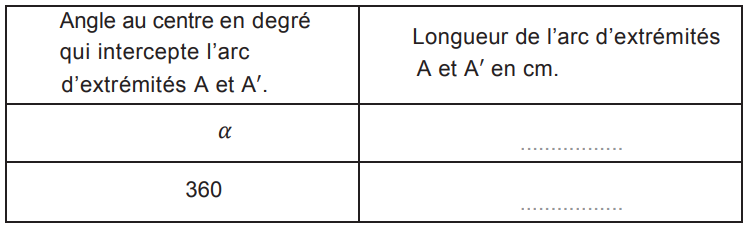
6. Construire, à l’échelle 1/2, le patron du saupoudreur.

Pages : 1 2