Le théorème de Pythagore

1-Calculer la racine carrée d’un nombre
a. Carré d’un nombre
Un nombre multiplié par lui-même est un nombre au carré → a²= a × a
Exemples :
❏ 5 au carré s’écrit 5² et il est égal à 5 × 5 = 25
❏ 7² = ……………………………………….……..
Les carrés parfaits sont les carrés des nombres entiers :

b. racine carré d’un nombre
a étant un nombre positif, √𝑎 est le nombre positif dont le carré est égal à a.
Par exemple la longueur du côté du carré ci-dessous est le nombre positif dont le carré est égal à 289 c’est donc √289
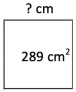
Comme 17² = 289, donc √289= 17
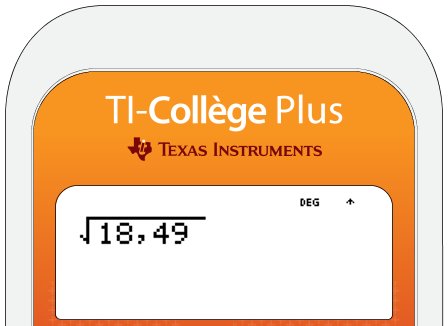
La touche de la calculatrice dite « racine carrée », permet d’obtenir les racines carrées des autres nombres décimaux ou rationnels.
Exemples :
❏ √18, 49 =
❏ √5 ≈
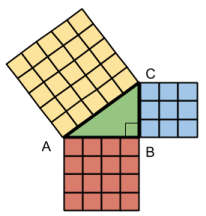
2-Calculer la longueur du côté d’un triangle rectangle
a. Activité
b. Vocabulaire
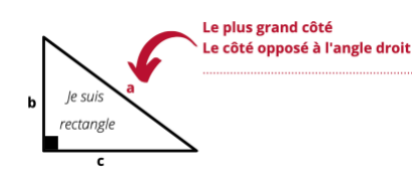
c. Théorème de Pythagore
Dans tout triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des 2 autres côtés.
Dans ce triangle rectangle ABC, on a la relation : AC² = AB² + BC²
c. Calculer une longueur avec le théorème de Pythagore
Exemple 1: (calcul de longueur de l’hypoténuse)
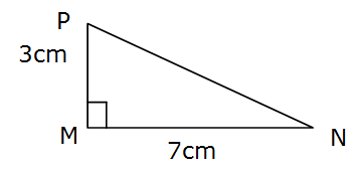
Le triangle MNP est rectangle en M tel que MN = 7 cm et MP = 3 cm.
Calculer la longueur NP.
On cherche l’hypoténuse
Solution
Le triangle MNP est rectangle en M.
D’après le théorème de Pythagore, on a NP² = MP² + MN²
NP² = 3² + 7²
NP² = 9 + 49 = 58
Donc NP = √ 58 ≈ 7, 6 cm (valeur arrondie au dixième du centimètre)
Exemple 2: (calcul de longueur d’un côté de l’angle droit)
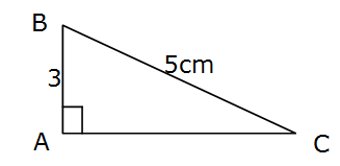
Le triangle ABC est rectangle en A tel que AB = 3 cm et BC = 5 cm.
Calculer la longueur AC.
On cherche un côté de l’angle droit
Solution
Le triangle ABC est rectangle en A, d’après le théorème de Pythagore, on a :
BC² = AB² + AC²
AC² = BC² – AB²
AC² = 5² – 3²
AC² = 25 – 9 = 16
AC = √ 16 = 4 cm