I- Activité :

Trace un triangle ABC tel que AB = 7 cm, BC = 4 cm et AC = 9 cm

1– Trace à l’aide du compas la médiatrice du [AB]

2– Trace à l’aide du compas la médiatrice du [BC]

3– Trace à l’aide du compas la médiatrice du [AC]

4– Que remaques-tu ?

5– Nomme O le point d’intersection des trois médiatrices puis trace le cercle de centre O et qui passe par A.

Que remarques-tu ?

II-Propriétés des médiatrices dans un triangle

Dans tous les triangles, les médiatrices des côtés se coupent en un seul point. Ce point est le centre du cercle circonscrit au triangle.

On dit qu’elles sont concourantes. ​

Le cercle passe par les 3 sommets,  on dit que le triangle est inscrit dans le cercle. ​

III-Cas particuliers

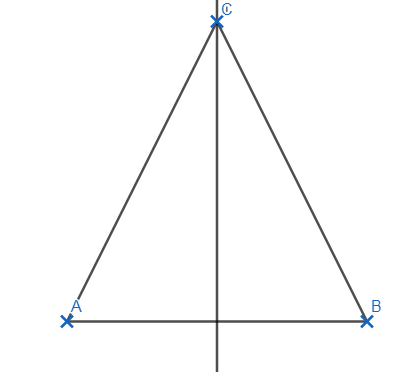
1-Triangle isocèle

Si un triangle ABC est isocèle en C, alors C appartient à la médiatrice du segment [AB] car il est équidistant des points A et B.

2-Triangle équilatéral

Dans un triangle équilatéral, chaque sommet appartient à la médiatrice du segment opposé à ce sommet.

---

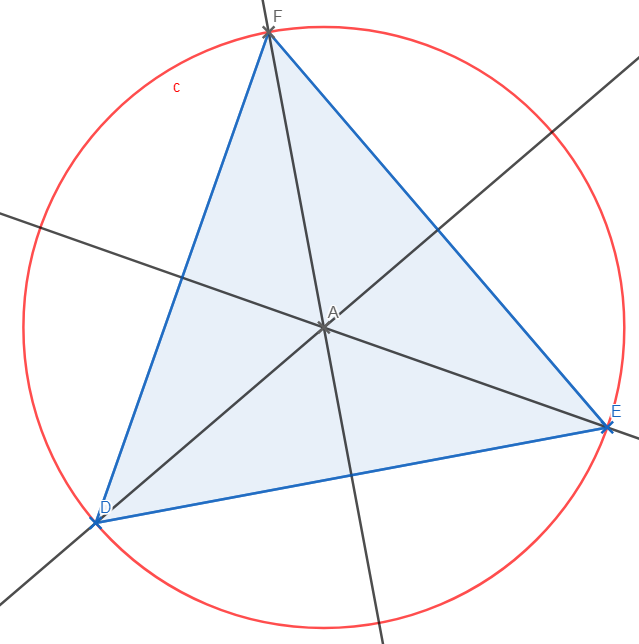
Construction des médiatrices des côtés d’un triangle ABC

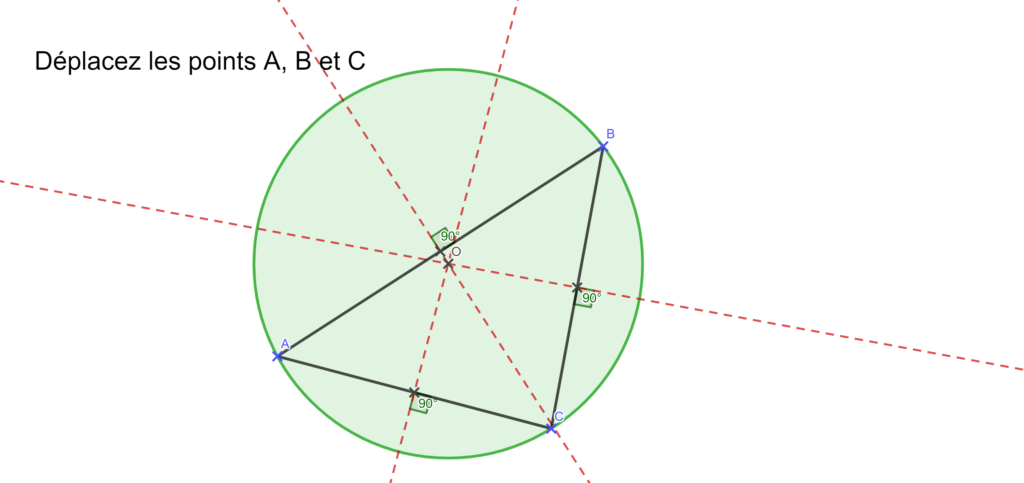
3-Triangle rectangle

Tracer un triangle ABC rectangle en B.

Tracer le cercle circonscrit au triangle ABC.

Que remarque-t-on ?

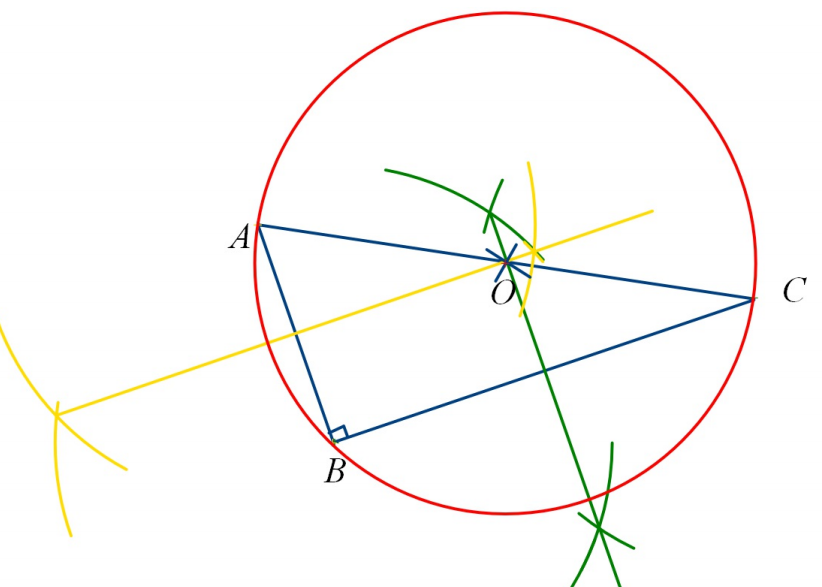
Réponse

Le cercle circonscrit au triangle rectangle a pour diamètre un des côtés du triangle.

---

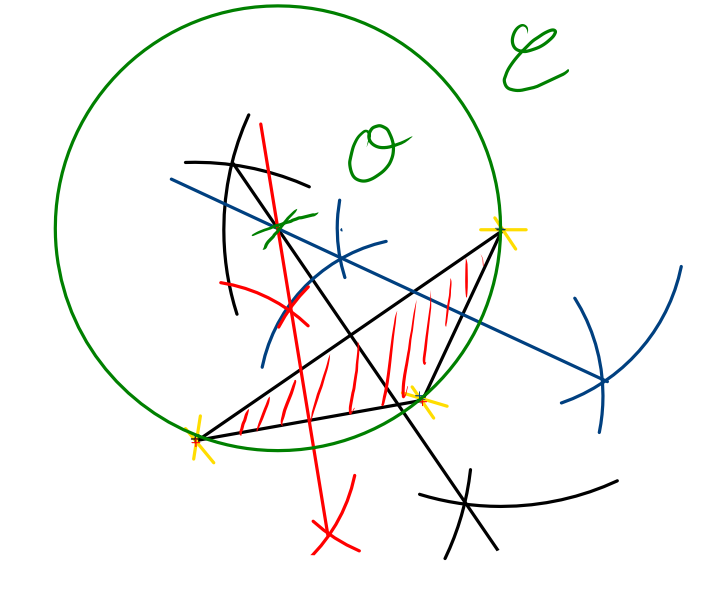
Activité réalisée avec GeoGebra : point équidistant à trois points

Comment placer un point O équidistant des points A, B et C (c’est à dire à égale distance des points A, B et C) ?

Pages : 1 2