1) Rappels : les angles dans un triangle

La somme des angles d’un triangle est égale à 180°.

​

Cas particuliers :​

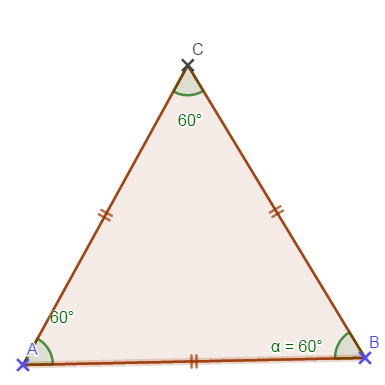
Dans un triangle équilatéral, les 3 angles sont égaux et mesurent 60°.​

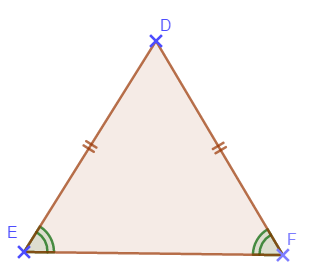
Dans un triangle isocèle, les deux angles adjacents à la base sont égaux.​

Dans un triangle rectangle, la somme des 2 angles aigus est 90°.​

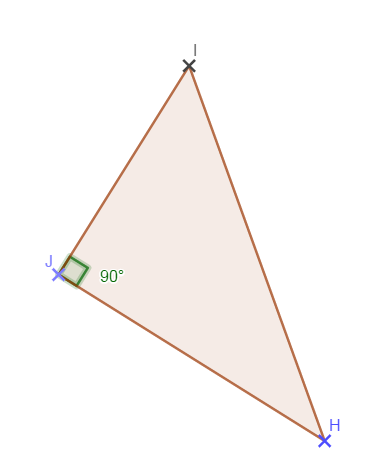
Î + Ĥ = 90°

2) Vocabulaire

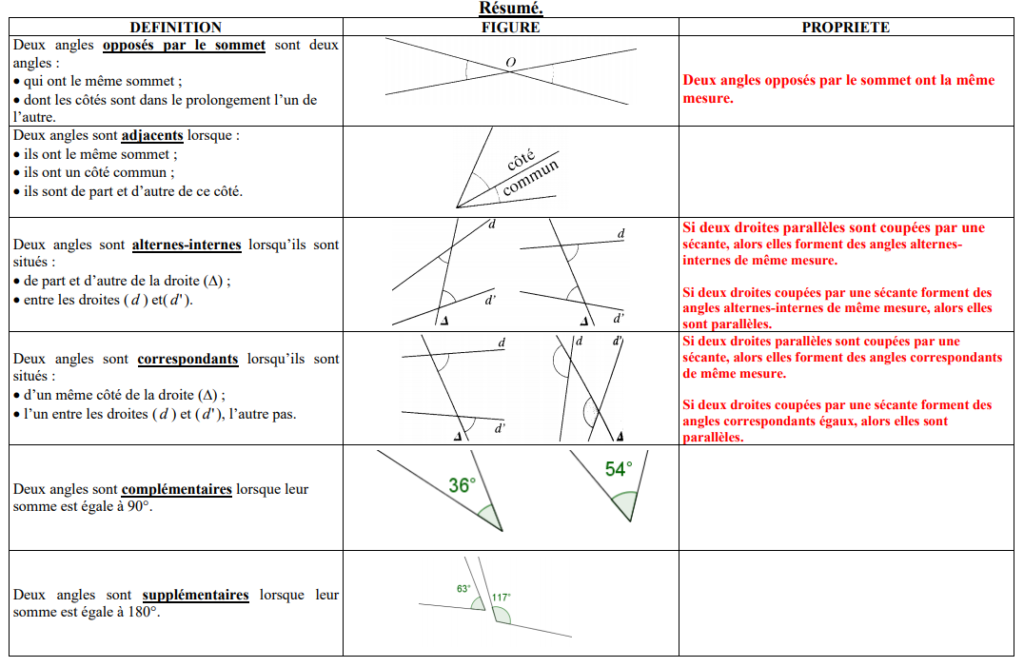
① Deux angles sont adjacents («qui se touchent») si​

• ils ont le même sommet,​

• ils ont un côté en commun, et se trouvent de part et d’autre de ce côté.​

 

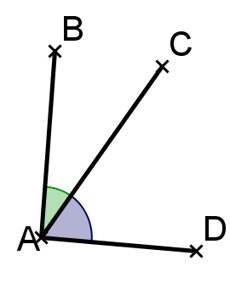
  BÂC et   CÂD sont deux angles sont adjacents.

② Deux angles sont complémentaires si leur somme est égale à 90°.​

Exemple : 

Dans un triangle rectangle, les deux angles aigus sont complémentaires.​

③  Deux angles sont supplémentaires si leur somme est égale à 180°.

Activité : Les angles n°1

④ Deux angles sont opposés par le sommet si :​

• ils ont le même sommet,​

• leurs côtés sont dans le prolongement l’un de l’autre.​

 

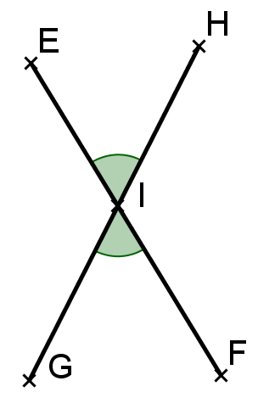
EÎH et GÎF sont deux angles opposés par le sommet.

Soit deux droites (d1) et (d2), coupées par une sécante (d).

​Pour revoir la leçon en vidéo :

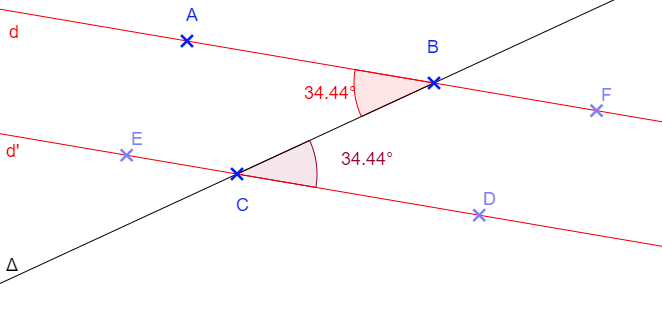
⑤ Deux angles alternes-internes sont situés entre (d1) et (d2) et de part et d’autre de (d).​

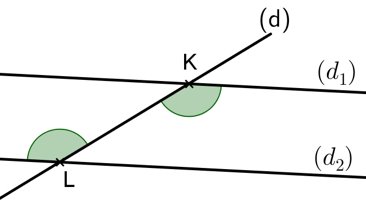
Angles alternes-internes

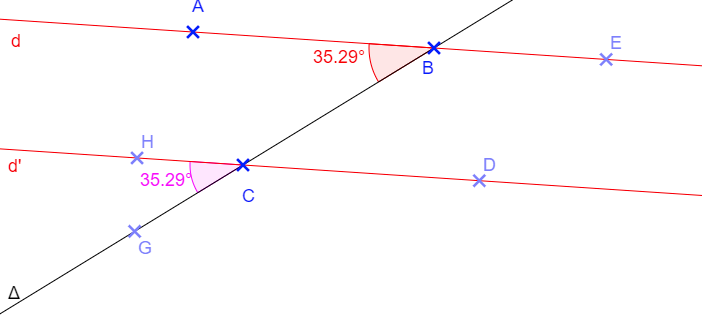
 ⑥  Deux angles correspondants sont situés du même côté de (d) et un seul est entre (d1) et (d2).​

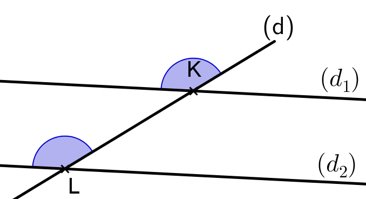
Angles correspondants

​Pour revoir la leçon en vidéo :

Activité : Les angles n°2

Activité : Les angles n°3

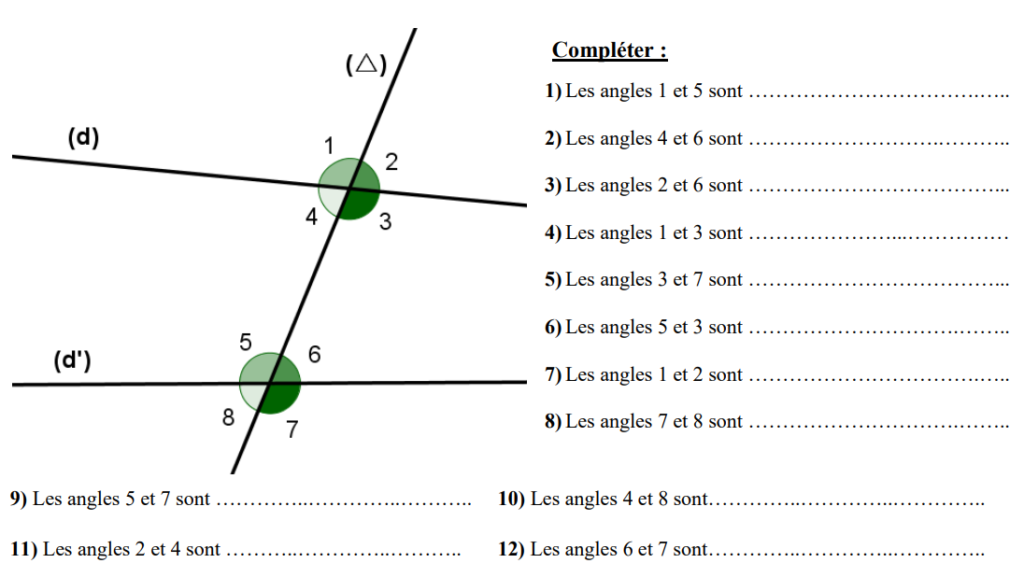
3) Propriétés

① Angles opposés par le sommet :​

Si deux angles sont opposés par le sommet alors ils ont la même mesure en degrés.​

 

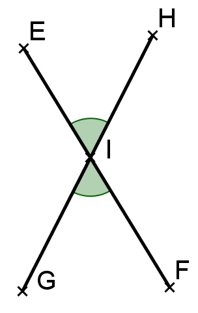
EÎH et GÎF sont dex angles opposés par le sommet donct ils sont égaux donc EÎH=GÎH

Activité : Les propriétés des angles n°1

② Angles alternes-internes :

• Si deux droites parallèles sont coupées par une sécante, alors les angles alternes-internes qu’elles forment ont la même mesure.

 

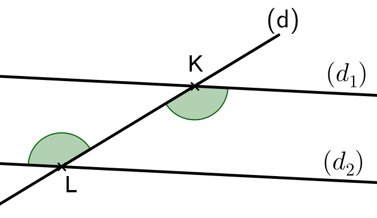
(d₁) // (d₂)

• Si deux droites coupées par une sécante forment deux angles alternes-internes de même mesure, alors ces droites sont parallèles.​

③ angles correspondants :

• Si deux droites parallèles sont coupées par une sécante, alors les angles correspondants qu’elles forment ont la même mesure.

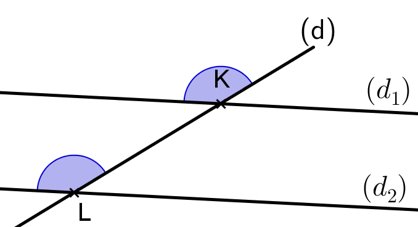
(d₁) // (d₂)

• Si deux droites coupées par une sécante forment deux angles correspondants de même mesure, alors ces droites sont parallèles.

Activité : Les propriétés des angles n°2 (la réciproque)

Propriétés droites parallèles et angles alternes-internes

Propriétés droites parallèles et angles correspondants

​Pour revoir la leçon en vidéo :

Pages : 1 2 3 4 5 6