Équation « Produit nul »
I-Activité

Résoudre les équations suivantes.
3𝒙 = 0
3(𝒙 – 2) = 0
𝒙(𝒙 + 3) = 0
(𝒙 + 4) (𝒙 – 5) = 0
II-Equation-produit nul A × B = 0
Si un produit est nul, alors un de ses facteurs est nul.
Si A × B = 0 alors A = 0 ou B = 0.
Exemple 1 :
Résoudre l’équation (2𝒙 – 5) (𝒙 + 7) = 0
(2𝒙 – 5) (𝒙 + 7) = 0
Si A × B = 0 alors A = 0 ou B = 0.
(2𝒙 – 5) = 0 ou (𝒙 + 7) = 0
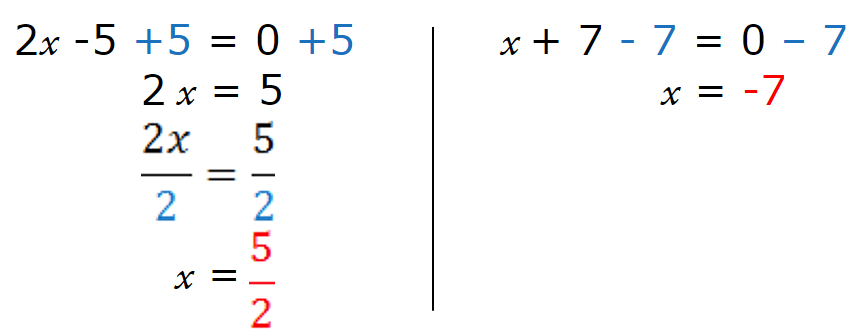

Exemple 2 :
Résoudre l’équation (4𝒙 + 1)² = 0
Cela revient à résoudre l’équation (4𝒙 + 1)(4𝒙 + 1) = 0
Si A × B = 0 alors A = 0 ou B = 0.
(4𝒙 + 1) = 0 avec la même équation en double
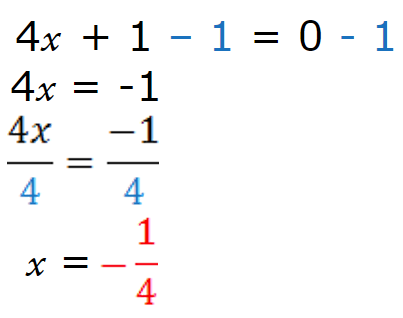

Exemple 3 :
Résoudre l’équation 𝒙² −5𝒙 = 0
Nous devons d’abord factoriser cette expression.
𝒙(𝒙 −5) = 0
Si A × B = 0 alors A = 0 ou B = 0.
Ce qui se traduit par 𝒙 = 0 ou (𝒙 − 5) = 0
Les solutions de l’équation sont donc S = {0 ; 5}
III-Equation 𝒙² = a
Premier cas a < 0 :
L’équation 𝒙² = a n’a pas de solutions car un carré est toujours positif.
Deuxième cas a > 0 :
𝒙² = a
𝒙² − a = 0 (1)
Nous devons ensuite factoriser cette expression à l’aide de l’identité remarquable a² − b² = (a − b)(a + b)
Or a = (√a)² donc l’équation (1) devient :
(𝒙 − √a)(𝒙 + √a) = 0 on peut donc appliquer la propriété du produit nul :
A × B = 0 alors A = 0 ou B = 0.
Ce qui se traduit par (𝒙 − √a) = 0 ou (𝒙 + √a) = 0
Les solutions de l’équation (1) sont donc S = {-√a; √a}
Exemple 4 :
𝒙² = 7
𝒙² − 7 = 0
𝒙² − (√7)² = 0
(𝒙 − √7)(𝒙 + √7) = 0
A × B = 0 alors A = 0 ou B = 0.
Ce qui se traduit par (𝒙 − √7) = 0 ou (𝒙 + √7) = 0
Les solutions de l’équation sont donc S = {-√7; √7}