I-Transformer une figure par une homothétie

Ces figures sont-elles superposables ? Justifie ta réponse.

Définition

Transformer une figure par une homothétie de centre O, c’est l’agrandir ou la réduire en faisant glisser ses points le long de droites passant par O.

Une homothétie est définie par :

  • un centre
  • un rapport k non nul

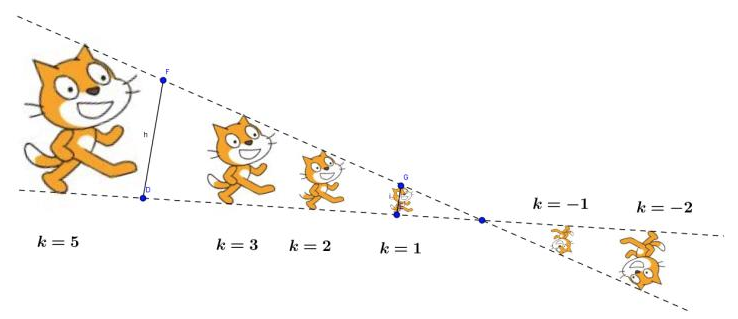
1) Homothétie de rapport positif

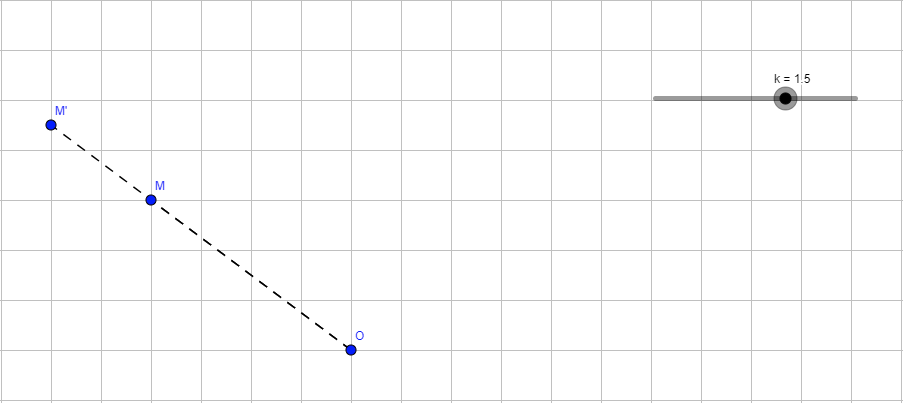
M’ est l’image de M par l’homothétie de centre O et de rapport 1,5 signifie que :

  • O, M et M’ sont alignés
  • M et M’ sont du même côté par rapport à O.
  • OM’ = 1,5 x OM autrement dit OM’/OM = 1,5

Application :

Place le point M’ image de M par l’homothétie de centre O et de rapport O,5.

Que remarque-t-on ?

Remarque :

Si k > 1, la distance OM’ est plus grande que la distance OM et le point M’ est plus éloigné que le point M du centre O.

Si O < k < 1, la distance OM’ est plus petite que la distance OM et le point M’ est plus proche que le point M du centre O.

2) Homothétie de rapport négatif

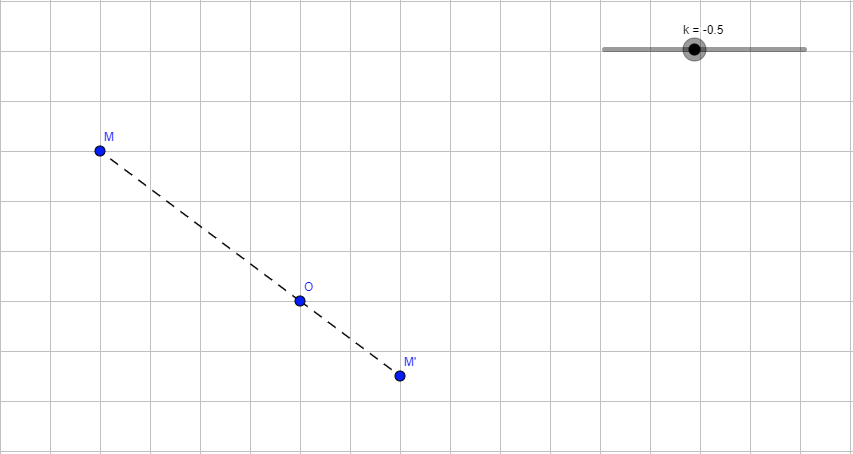
M’ est l’image de M par l’homothétie de centre O et de rapport -0,5 signifie que :

  • O, M et M’ sont alignés
  • M et M’ ne sont pas du même côté par rapport à O.
  • OM’ = 0,5 x OM

3) Activité

Partie 1

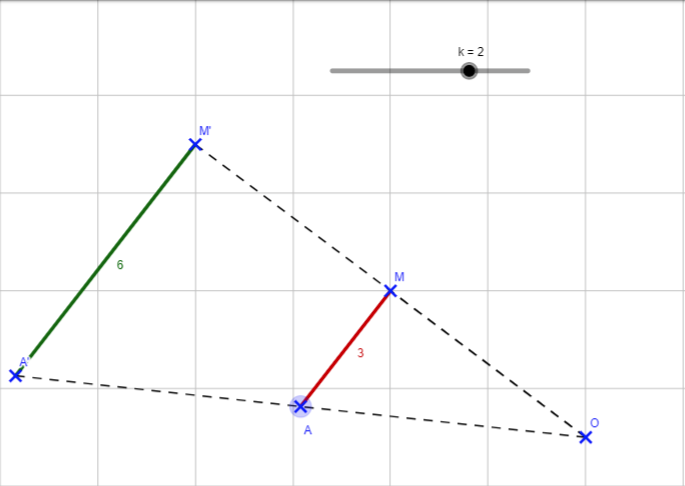
  • Tracer un segment [AM] de longueur 3 cm et placer un point O.
  • Tracer le segment [A’M’] image du segment [AM] par l’homothétie de centre O et de rapport 2.
  • Que remarque-t-on au niveau de la longueur A’M’ ?
  • Que peut-on dire des segments [A’M’] et [AM] ?

Partie 2

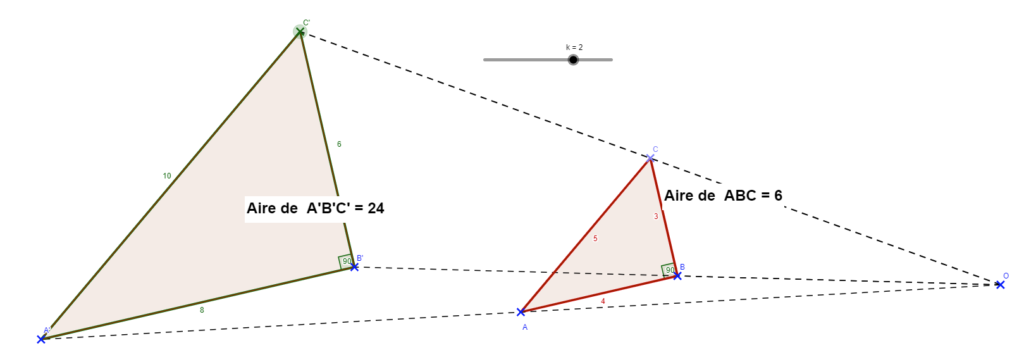
  • Tracer un triangle ABC rectangle en A tel que AB = 4 cm, BC = 5 cm et AC = 3 cm.
  • Placer un point O puis tracer le triangle A’B’C ‘ image du triangle ABC par l’homothétie de centre O et de rapport 2.
  • Que remarque-t-on ?
  • Calculer l’aire du triangle ABC et l’aire du triangle A’B’C’, que peut-on conjecturer ?

4) Propriétés

  • Une figure et son image par une homothétie ont la même forme.
  • L’homothétie conserve les alignements et les angles.
  • L’image d’une droite est une droite qui lui est parallèle.
  • L’image d’un segment est un segment qui lui est parallèle.

Si K est positif : nous avons deux cas :

  • Si k > 1, la figure subit un agrandissement.
  • Si O < k < 1, la figure subit une réduction.

Si K est négatif, la figure est renversée et nous avons deux cas :

  • Si -k > 1, la figure subit un agrandissement.
  • Si O < -k < 1, la figure subit une réduction.
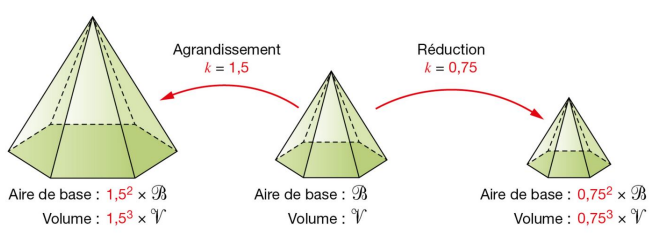
  • Les longueurs sont multipliées par k (ou par -k si k < 0).
  • Les aires sont multipliées par k².
  • Les volumes sont multipliées par k3 (ou par -k si k < 0).

Exercices d’application

Pour télécharger le document

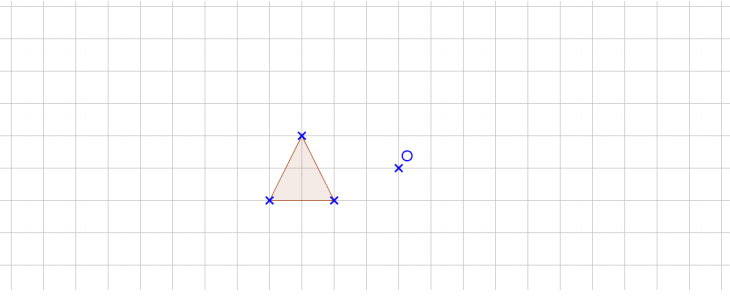
Application 1

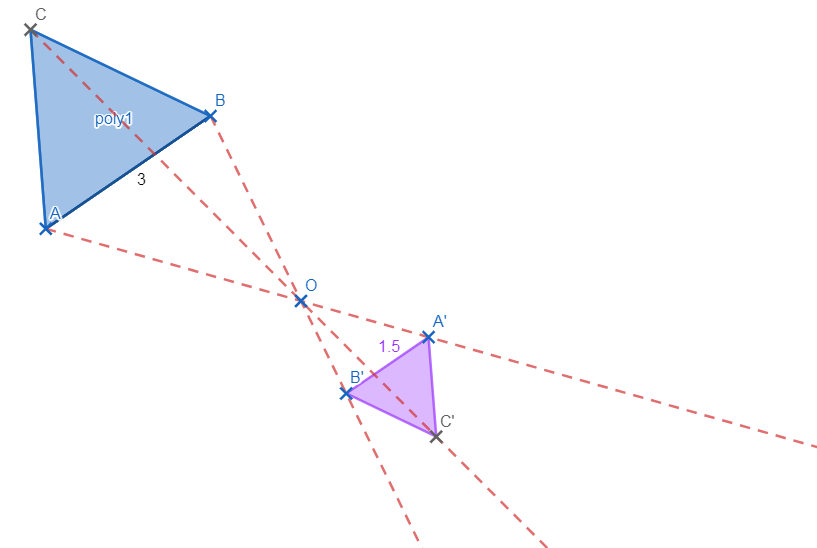
Construis les images du triangle par les homothéties de centre O et de rapports 3 ; -1 et -2.

Remarque :
L’image du triangle de départ par l’homothétie de centre O et de rapport -1 est aussi l’image de ce triangle par la symétrie
centrale de centre O : une homothétie de centre O et de rapport -1 est une symétrie centrale de centre O.

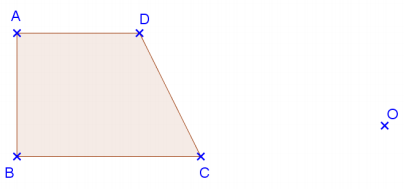
Application 2

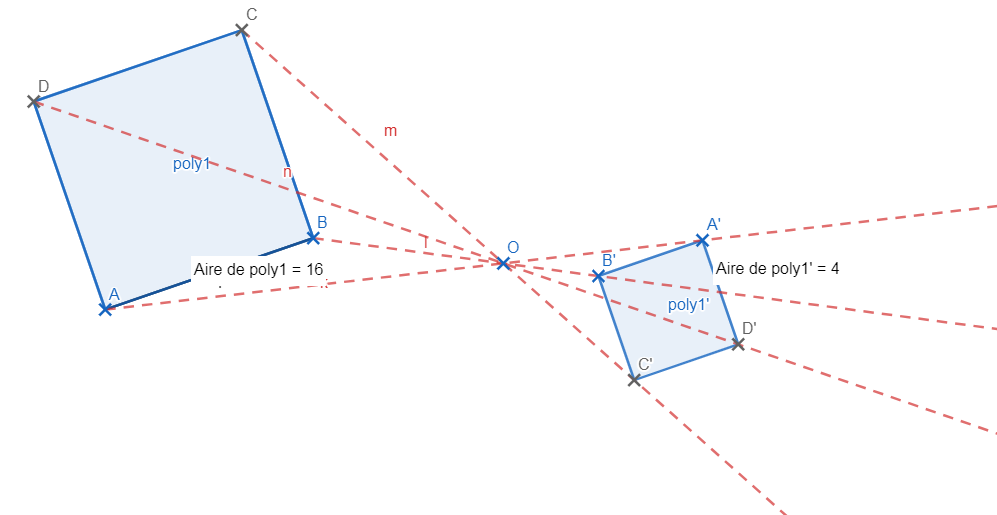
Construis les images du trapèze rectangle ABCD par les homothéties de centre O et de rapports 5/2 et –0,8.

Application 3

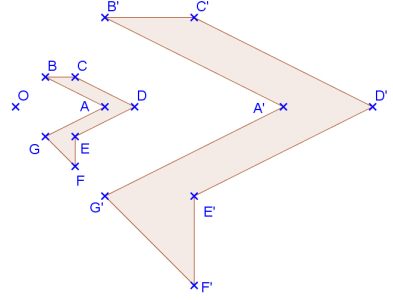
Le périmètre du polygone ABCDEFG est 12 cm, et son aire est 2,5 cm².
A’B’C’D’E’F’G’ est l’image de ABCDEFG par l’homothétie de rapport 3 et de centre O.
Complète :
A’B’C’D’E’F’G’ est …………………………..de ABCDEFG.
Le périmètre de A’B’C’D’E’F’G’ est ……………………
L’aire de A’B’C’D’E’F’G’ est ………………………

II- Triangles semblables

Pour télécharger le document

Définition :

Deux triangles sont dits semblables lorsque leurs angles sont égaux deux à deux. 

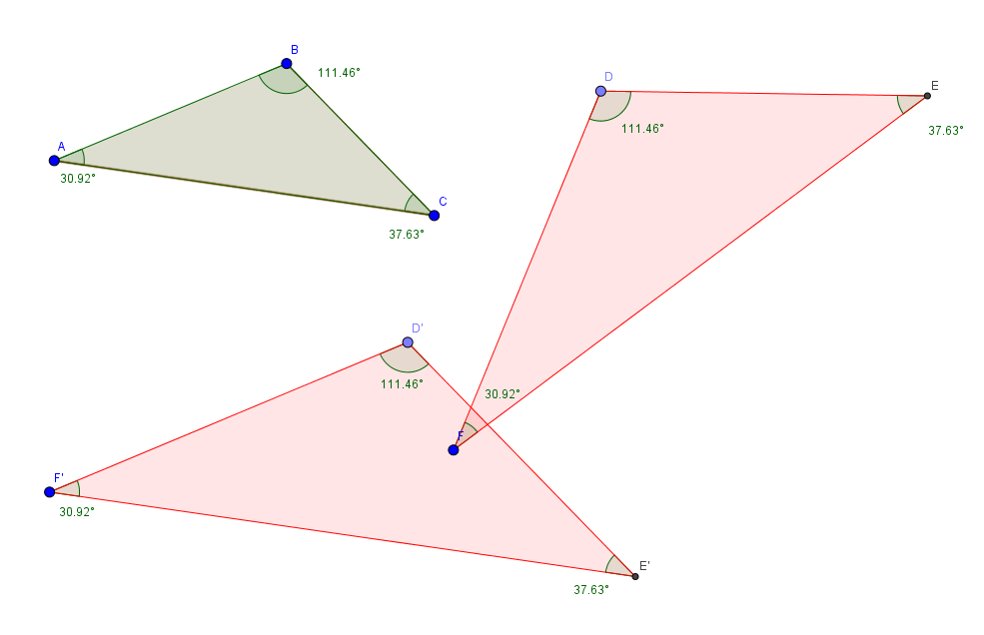
Méthode :

Il suffit de repérer deux angles égaux deux à deux.​

​Le troisième couple le sera aussi car la somme des angles dans un triangle est égale à 180°.​

Propriétés :

Si deux triangles sont semblables alors les côtés opposés aux angles égaux ont des longueurs deux à deux proportionnelles.

Exemple :

Les triangles NOM et PQR sont semblables alors les côtés opposés aux angles
égaux ont des longueurs deux à deux proportionnelles.

 

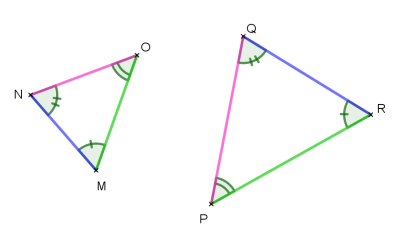
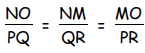
[NQ] et [PQ] sont les côtés opposés aux deux angles égaux, on les appelle deux côtés homologues, les angles et les sommets associés sont également appelés angles homologues et sommets homologues.

Réciproquement : si deux triangles ont leurs côtés proportionnels deux à deux. alors ils sont semblables.

Exemple :

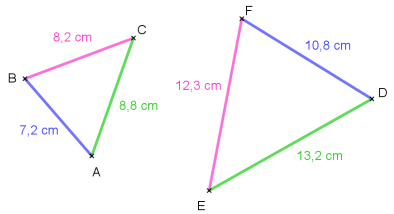
Les triangles ABC et EFG sont-ils semblables ?

On range les longueurs des triangles dans l’ordre croissant.

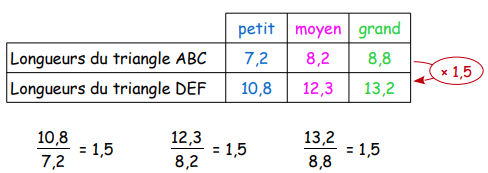
Les quotients sont égaux donc longueurs des côtés des triangles sont proportionnelles. Ainsi les triangles ABC et DEF sont semblables.

Activités :

Pour télécharger le document

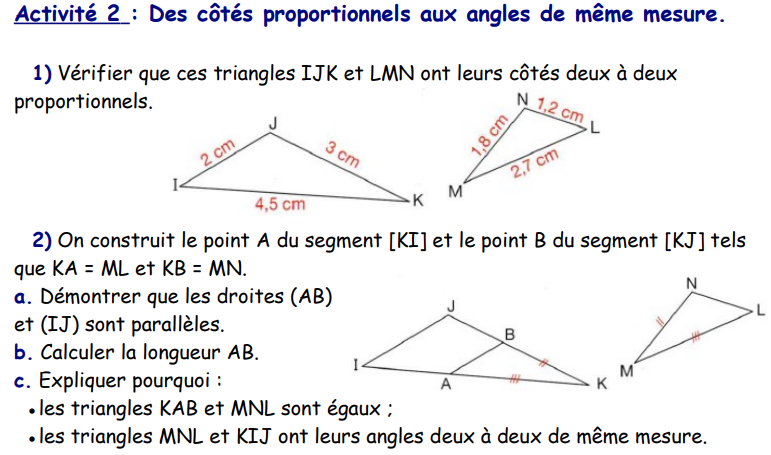
Activité 1

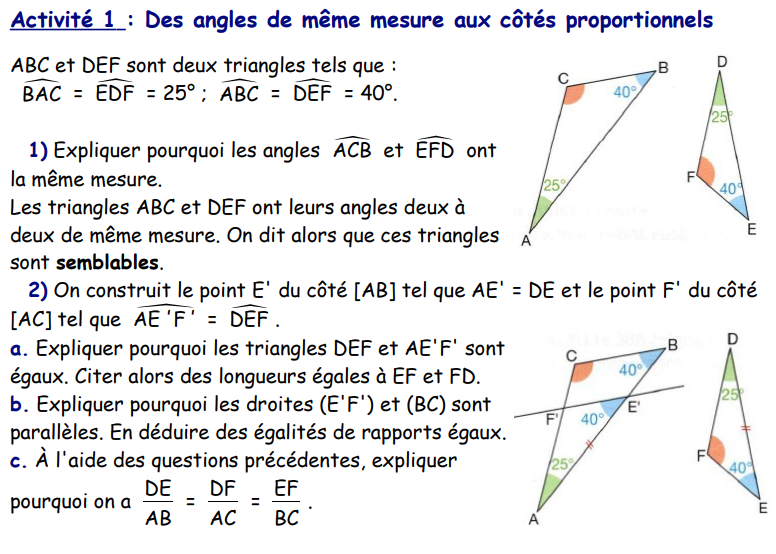
Activité 2

 

Enigmes : Qui a kidnappé le chat de Mme Fonchain ?

Pages : 1 2 3