Opérations avec les nombres fractionnaires

I-Activité

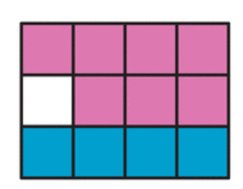
Donner la fraction équivalente à la partie rose.
Donner la fraction équivalente à la partie bleue.
Calculer alors la somme suivante.
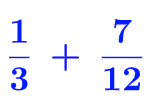
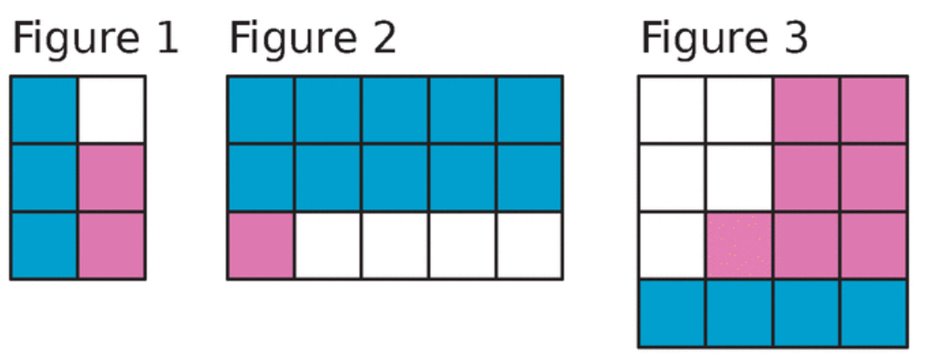
En t’inspirant de situation précédente, écris les égalités fractionnaires correspondantes.
II-Somme ou différence de 2 fractions
La somme de 2 fractions sert à calculer le total de 2 parties du même objet.
La différence de 2 fractions sert à calculer la différence de 2 parties du même objet.
Règles :
1- On ne peut pas ajouter 2 fractions de dénominateurs différents.

2- Quand les dénominateurs sont égaux, on ajoute uniquement les numérateurs.
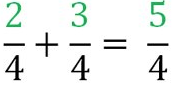
3- Mêmes règles pour soustraire.
En lettres
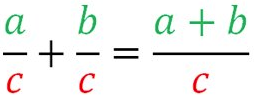
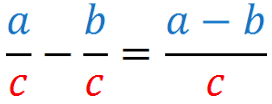
Remarques :
c ≠ 0 car on ne peut pas diviser par zéro !
Quand les dénominateurs sont différents, il faut les convertir pour les rendre identiques, on dit qu’on réduit les fractions au même dénominateur.
Exemple 1 : (somme de deux fractions ayant le même dénominateur)
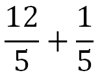
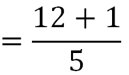
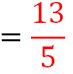
Exemple 2 : (somme de deux fractions avec des dénominateurs différents mais multiples)
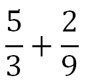
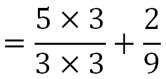
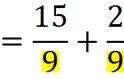
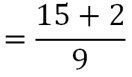
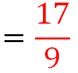
Exemple 3 : (somme de deux fractions avec des dénominateurs différents et non multiples)
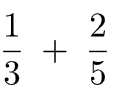
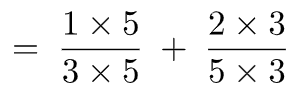
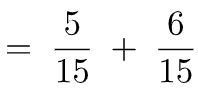
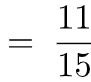
Exemple 4 : (soustraction de deux fractions ayant le même dénominateur)
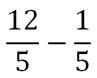
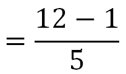
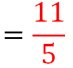
Exemple 5 : (soustraction de deux fractions avec des dénominateurs différents)
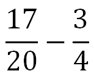
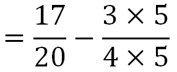
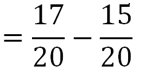
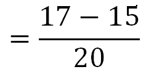
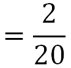
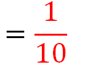
Pour revoir la leçon en vidéo
III-Comparaison de 2 fractions
Pour comparer deux fractions, on procède de la même manière, si nécessaire on réduit les fractions au même dénominateur puis on compare les numérateurs.
Exemple 1 : (comparaison de deux fractions avec le même dénominateur)
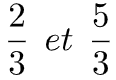
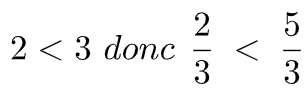
Exemple 2 : (comparaison de deux fractions ayant des dénominateurs différents)
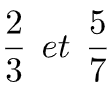
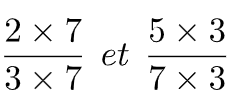
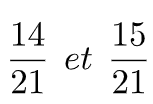
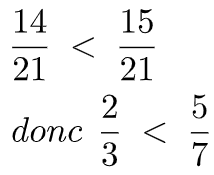
IV-Comparaison de fraction à 1
– Si le numérateur est supérieur au dénominateur alors la fraction est supérieure à 1.
– Si le numérateur est inférieur au dénominateur alors la fraction est inférieure à 1.
– Si le numérateur est égal au dénominateur alors la fraction est égale à 1.
Exemple :
