Calcul de volume
Activité

Les confitures produites par un artisan sont conditionnées dans des pots de deux types : pot n°1 et pot n°2.


Les pots sont remplis au maximum à 90 % de leur volume.
1. Le pot n°1 est un cylindre, de hauteur 8 cm et de diamètre 7 cm.
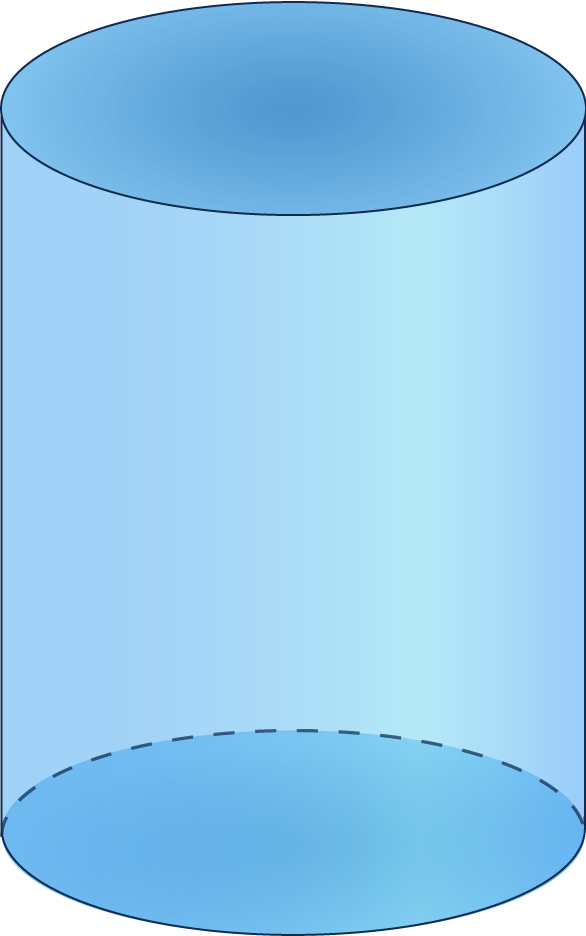
a. Déterminer le volume du pot n°1, en centimètre cube, arrondir à l’entier.
b. Quel volume maximum de confiture, en centimètre cube, arrondir à l’entier,
peut-il contenir ?
2. Le pot n°2 est un prisme (figure A) dont la base (la figure B) est un hexagone régulier de centre O.
Sa hauteur est de 8 cm et les côtés de l’hexagone régulier mesurent 4 cm.

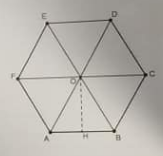
On admet que les six triangles OAB, OBC, OCD, OEF et OFA sont des triangles équilatéraux.
On admet également que l’aire d’un triangle équilatéral ayant des côtés de longeur 𝑥 est :
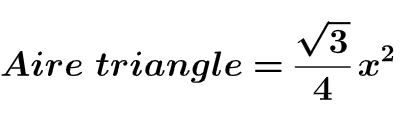
a. Montrer que l’aire de l’hexagone ABCDEF est égale à 24√3cm²
b. En déduire le volume du pot n°2, en centimètre cube, arrondi à l’entier.
c. Quel volume maximum de confiture, en centimètre cube, arrondi à l’entier peut-il contenir ?