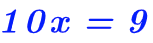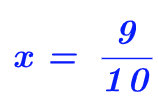Equation du 1er degré

I – Définition
Une équation du premier degré à une inconnue est une égalité où figure un nombre inconnu qu’on voudrait connaitre.
Une équation admet deux membres.
Résoudre une équation, c’est trouver le ou les nombres qui rendent l’égalité vraie quand ils remplacent 𝒙.
Une équation du 1er degré, à une inconnue [avec des « 𝒙 » et pas de « 𝒙² »], a en général 1 seule solution.
Exemple 1
Pour l’équation : 3𝒙 + 7 = 2𝒙
(-1) n’est pas une solution de cette équation car 3 x (-1) + 7 ≠ 2 x (-1).
En revanche (-7) est solution car 3 x (-7) +7 = 2 x (-7)
II – Propriétés élémentaires
C’est le principe de la balance Roberval.
On souhaite par exemple résoudre l’équation : 2𝒙 + 1 = 111
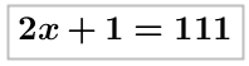
a- On ne change pas une égalité si on ajoute (ou on soustrait) un même nombre aux deux membres de cette égalité.
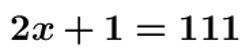
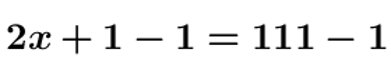
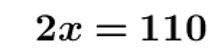
b- On ne change pas une égalité si on multiplie (ou on divise) les deux membres de cette égalité par un même nombre non nul.
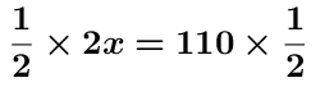
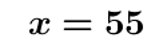
Exemple 2
Résoudre les équations suivantes.
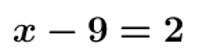
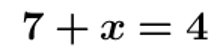
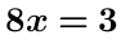
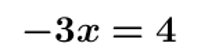
III – Equation à plusieurs opérations
On les annule une par une, en commençant par les additions/soustractions.
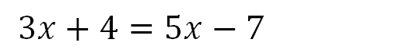
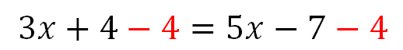
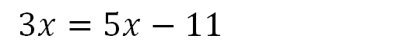
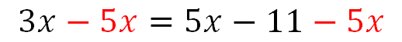
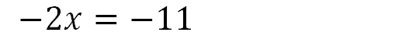
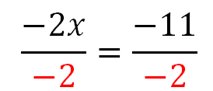
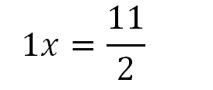
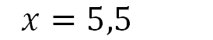
Exemple 3
Traduis ce problème par une équation puis résoudre.

Exemple 4
Traduis ce problème par une équation puis résoudre.
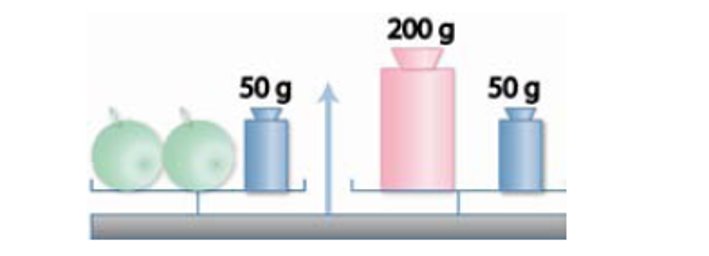
Exemple 5
Traduis ce problème par une équation puis résoudre.
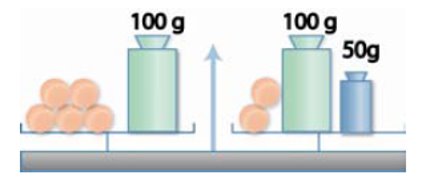
Exemple 6 (pour aller plus loin)
Traduis ce problème par une équation puis résoudre.

IV – Equation quotient
On souhaite résoudre l’équation quotient ci-dessous :
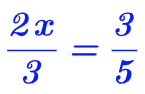
On effectue d’abord le roduit en croix pour se ramener à un cas classique d’une équation du premier degré
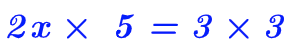
On réduit l’expression puis on résoud l’équation