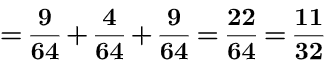Calcul de probabilités

Activité :
Lancer d’une pièce
Sur une pièce de monnaie, on appelle « Pile » la face commune à tous les pays de la zone euro et « Face » l’autre.

Que pensez-vous des affirmations suivantes à propos du jeu de Pile ou Face ?
« On a une chance sur deux d’obtenir Pile. »
« On obtient Pile une fois sur deux. »
Simulation d’un lancer d’une pièce à l’aide du tableur
Pour avoir un nombre aléatoire décimal entre 0 et 1 avec un tableur, il suffit de saisir la formule =ALEA()

Pour avoir un nombre aléatoire dans une liste, par exemple 1ou 2, il suffit de saisir la formule =ALEA.ENTRE.BORNES(1;2)

Simulation de 10 lancers
On simule le lancer d’une pièce de monnaie non truquée 10 fois de suite et on note les résultats dans un tableau.
A chaque fois qu’on appuie sur la touche F9, on génère un nouveau tirage.
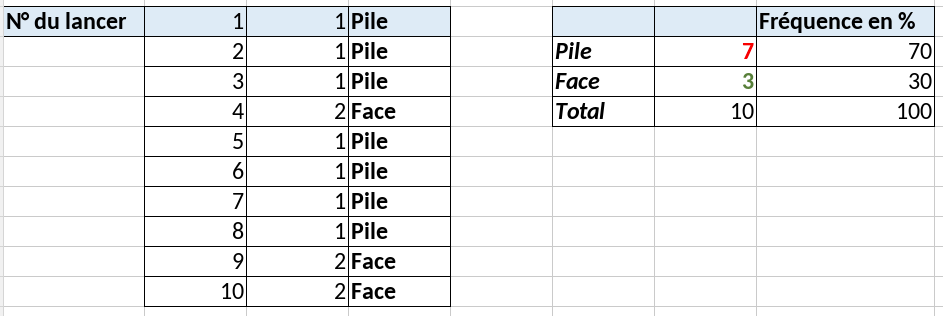
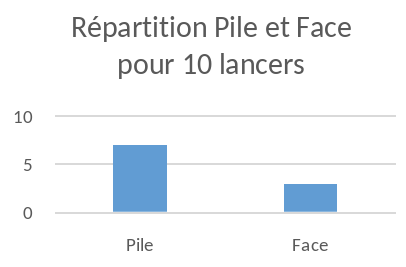
La répartition est-elle normale ?
La pièce est-elle truquée ?
Si on lance la même pièce une fois de plus, laquelle des affirmations suivantes sera correcte ?
a. On a autant de chances d’obtenir Pile que Face.
b. On a plus de chances d’obtenir Pile.
c. On a plus de chances d’obtenir Face.
d. On ne peut pas obtenir à nouveau Face.
Simulation de 1 000 lancers
A partir du fichier « Simuler un lancer d’une pièce », reproduis le tableau en le copiant dans une autre feuile de calcul, puis modifie le pour simuler 500 puis 1 000 lancers.
Comment va évoluer la répartition des issues ?
Probabilités

I : Définition d’une expérience aléatoire
Une expérience aléatoire est une expérience renouvelable à l’identique, dont les résultats possibles sont connus sans qu’on puisse déterminer lequel sera réalisé.
Exemples :

Les résultats possibles sont : 1, 2, 3, 4, 5 ou 6.

Les résultats possibles sont : Pile ou Face.

Nous avons 52 résultats possibles, 2 couleurs possibles et 4 motifs possibles (Trèfles, Carreau, Cœur et Piques)
II : Vocabulaire
Les résultats possibles s’appellent des issues.
Un événement est un ensemble d’issues.
Un événement élémentaire est un évènement qui ne contient qu’une seule issue.
La probabilité d’un événement estime la chance de se produire.
Exemple :
Les issues possibles d’un lancer de dé à six faces sont :
{ 1 ; 2 ; 3 ; 4 ; 5 ; 6}
Obtenir un nombre pair est un événement dont les issues possibles sont :
{ 2 ; 4 ; 6 }.
Obtenir un 6 est un événement élémentaire car il n’y a qu’une seule issue possible pour le réaliser.
III : Propriétés
Une probabilité est un nombre compris entre 0 et 1.
Plus la probabilité est proche de 1, plus l’événement a de chance de se réaliser.
Si elle est égale à 1, l’événement est appelé l’événement certain.
Un événement dont la probabilité est nulle est appelé l’événement impossible.
Exemple :
Obtenir un « 7 » avec un lancer de dé à 6 faces est un événement impossible car la probabilité de réaliser cet événement est nulle, P (Obtenir un « 7 ») = 0
Définition :
Une situation d’équiprobabilité est une expérience où toutes les issues ont la même chance de se produire.
Dans le cas d’un lancer de dé équilibré à six faces toutes les issues ont la même chance de se produire.
En cas d’équiprobabilité :
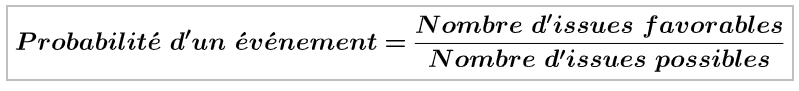
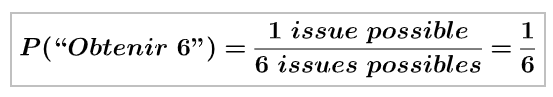
Remarque :
La somme de toutes les probabilités est toujours égale à 1.
Probabilités-Notion et vocabulaire
TD1 : série d’exercices
Correction du TD1
IV : Arbre des probabilités

Activité :
On tire au hasard une boule dans une urne qui contient 3 boules rouges, 3 boules bleues et 2 boules vertes.

On répète l’expérience deux fois de suite en remettant la boule dans l’urne, quelle est la probabilité de tirer deux boules de même couleur ?
On modélise d’abord cette expérience (de tirage avec remise) par un arbre des possibles dit aussi un arbre des probabilités.
On met sur chaque branche la probabilité de l’issue correspondante.
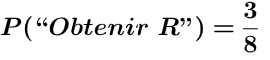
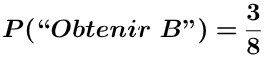
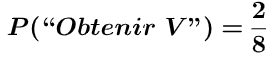
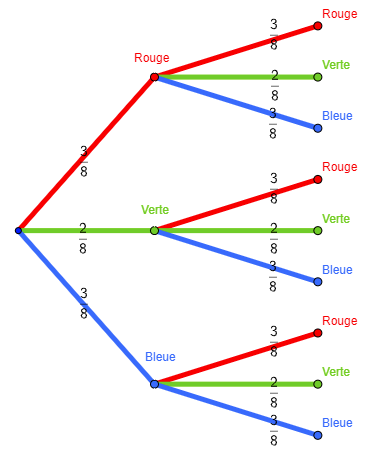
Notre expérience est répétée deux fois, l’arbre contient 9 chemins possibles.
Pour calculer la probabilité d’un chemin, on multiplie les probabilités sur les branches qui constituent ce chemin.
Pour calculer la probabilité de tirer une verte au premier tirage et une verte au deuxième tirage, il suffit de suivre le chemin permettant de réaliser cette issue et multiplier les probabilités correspondantes, on a alors :
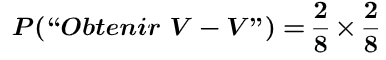
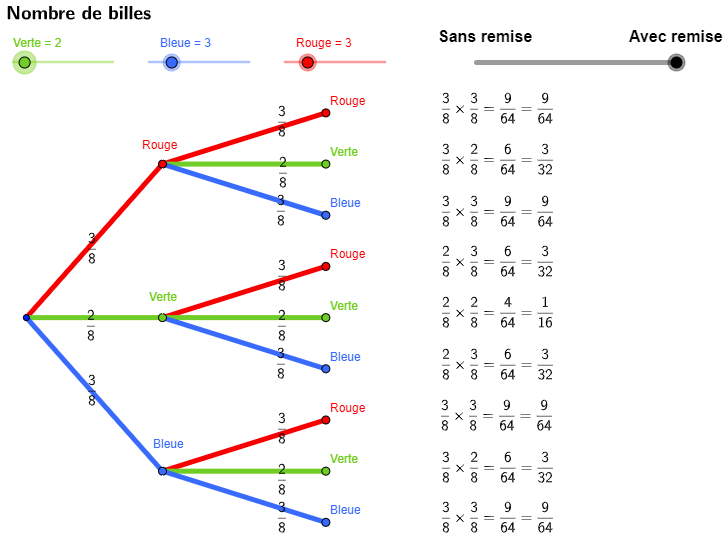
Quelle est la probabilité de tirer deux boules de même couleur ?
L’événement « Tirer deux boules de même couleur » a 3 issues possibles :
-Une rouge au premier tirage et une rouge au deuxième tirage.
ou
-Une verte au premier tirage et une verte au deuxième tirage.
ou
-Une bleue au premier tirage et une bleue au deuxième tirage.
Probabilité de tirer deux boules de même couleur
= Probabilité de (Tirer deux boules rouges ou deux boules vertes ou deux boules bleues)
= Probabilité de (Tirer deux boules rouges) + Probabilité de (Tirer deux boules vertes) + Probabilité de (Tirer deux boules bleues)