Fiche d’exercices

Exercice corrigé : évaluer une expression littérale

Exercice corrigé : programme de calcul et expression littérale

Exercice 1: Réduire, si possible, les expressions suivantes.

1. A = 11𝒙−4𝒙
2. B = 4𝒙×8𝒙
3. C = −5+2𝒙
4. D = −11𝒙+0
5. E = 2𝒙²−2𝒙²
6. F = −7𝒙−2
7. G = 9𝒙−9
8. H = 6𝒙²−6
9. I = −4𝒙×0

Exercice 2 : Simplifier les expressions suivantes.

1. 4×𝒙×2×𝒙×𝒙
2. (2+𝒙)×9
3. 7 + 𝒙×𝒙×𝒙
4. 𝒙 + 2𝒙+2
5. 6×𝒙×𝒙×7
6. 7x𝒙x𝒙x7
7. 7×𝒙×𝒙 + 8
8. 5×𝒙×𝒙×𝒙 + 4
9. 𝒙x𝒙 + 6
10. 4 + 𝒙×𝒙×7

Exercice 3 : Simplifier les expressions suivantes.

A=−(6𝒙−6)+(−7𝒙−3)

B=−(5𝒙−7)+(10𝒙²−7𝒙+11)

C=(−9𝒙+8)−(3𝒙+3)

D=−(6𝒙²−5𝒙+5)+(−𝒙²−6𝒙−10)

E=(7𝒙²+9𝒙−7)−(−8𝒙²+5𝒙−1)

F=(−2𝒙−2)−(6𝒙²−6𝒙+9)

Exercice 4 : Tester les égalités suivantes.

1. Tester l’égalité 5𝒙 + 6 = 6𝒙−3 pour 𝒙=9 puis pour 𝒙=2
2. Tester l’égalité 10(𝒙−3) = 4(2𝒙+1) pour 𝒙=2  puis pour 𝒙=17
3. Tester l’égalité 3𝒙−1=2𝒙+6  pour 𝒙=6  puis pour 𝒙=7

Exercice 5 : Développer et réduire les expressions suivantes.

1. A = 7(3𝒙+3)
2. B = 6(8𝒙+4)
3. C = 3(2𝒙+2)
4. D = 8(9𝒙+7)
5. E = 11(𝒙+4)

Exercice 6 : Développer et réduire les expressions suivantes.

1. A = 11(4𝒙−7)
2. B = −9(4𝒙+9)
3. C = −4(2𝒙 − 7)
4. D = 11(−9𝒙+1)
5. E = 5(−2𝒙 −3)

Exercice 7 : Réduire les expressions suivantes.

Les expressions en bout de ligne ou de colonne sont les sommes des expressions contenus dans la ligne ou la colonne.
Compléter la grille avec des expressions qui conviennent (plusieurs solutions possibles).

Exercice 8 : Démontrer l’équivalence de deux programmes de calcul.

On considère les programmes de calcul suivants :

Programme A :
– choisir un nombre,
– le tripler,
– puis enlever 66.

Programme B :
– choisir un nombre,
– lui soustraire 55,
– multiplier le résultat par 3,
– ajouter 99.

1) Tester ces programmes avec le nombre −3 et en choisissant un autre nombre quelconque. Émettre une conjecture.
2) Prouver cette conjecture.

Exercice 9 : Justifier si les nombres suivants sont solutions ou non des équations données

1. 10(𝒙−3) = 4(2𝒙+2) pour 𝒙 = 8 puis pour 𝒙 = 19
2. 40𝒙−240 = 10𝒙²−60𝒙 pour 𝒙 = 5, pour 𝒙 = 6  puis pour 𝒙 = 4
3. 8𝒙−56 = 𝒙²−7𝒙 pour 𝒙=8  , pour 𝒙 = 5  puis pour 𝒙 = 7
4. 8𝒙+6 = 9𝒙−3 pour 𝒙=9  puis pour 𝒙 = 2
5. 19−2𝒙 = 7+2𝒙 pour 𝒙=3  puis pour 𝒙 = 8

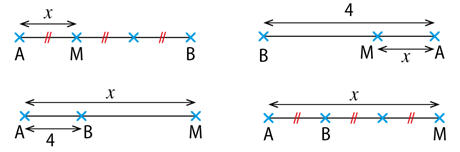
Exercice 10 :

Pour les quatre situations, M est un point sur la droite (AB) tel que AM = 𝒙

Dans chaque cas, exprimer la longueur MB en fonction de 𝒙.

Exercice 11 :

M est un point du segment [AB] tel que AM = 𝒙, ABCD est un rectangle.

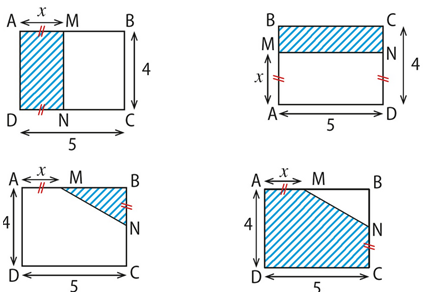
Dans chaque cas :   

a. Exprimer le périmètre de la partie hachurée en fonction de 𝒙.

b. Exprimer l’aire de la partie hachurée en fonction de 𝒙.

Pages : 1 2 3