Trigonométrie
Exercices

Exercice 1
Donne la valeur arrondie au degré de 𝒙.
sin 𝒙 = 0,24 ; cos 𝒙 = 0,5 ; tan 𝒙 = 1 ; cos 𝒙 = 0,75 ; tan 𝒙 = 4
Exercice 2
UVB est un triangle rectangle en B tel que BV = 2 cm et UV = 3,5 cm.
Calcule la mesure arrondie au degré de chacun des angles de ce triangle.
Exercice 3
Dans chaque cas, calcule la mesure de l’angle MN̂O ; donne la valeur arrondie au degré.
a-
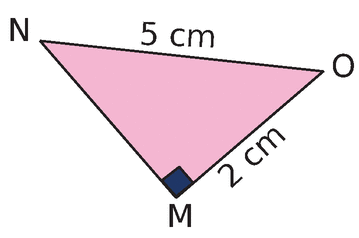
b-
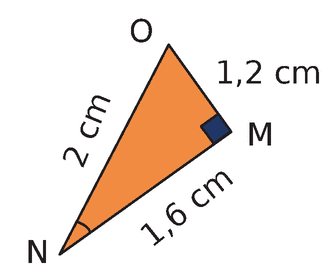
c-
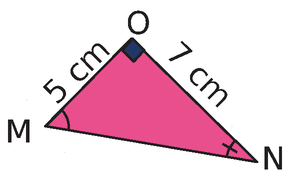
d-

Exercice 4

a- Calcule la mesure de l’angle IĜH.
b- Déduis-en la mesure de l’angle EĜF.
c-Calcule les longueurs EF et FG arrondies au dixième.
Exercice 5
MOI est un triangle tel que MO = 15 cm, OI = 25 cm et IM = 20 cm.
a- Ce triangle est-il rectangle ? Justifie ta réponse.
b- calcule la mesure arrondie au degré de chacun des angles de ce triangle.
Exercice 6
MAI est un triangle isocèle tel que MI = 5 cm, la hauteur [AH] mesure 3 cm.
Calcule la mesure arrondie au degré de chacun des angles de ce triangle.
Exercice 7
Pour chaque question, justifie la construction sans rapporteur.
a- Construis un angle  tel que tan  = 8/9
a- Construis un angle  tel que sin  = 0,6
Exercice 8 (extrait de brevet)
AHC est un triangle rectangle en H. La droite passant par A et perpendiculaire à la droite (AC) coupe (HC) en B.
On sait que AH = 4,8 cm et HC = 6,4 cm
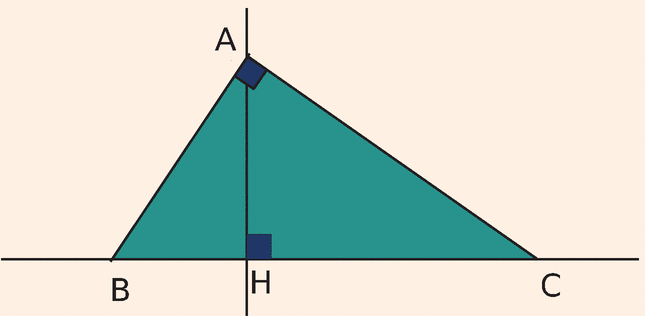
a- Justifie l’égalité : AĈH = 90° – HÂC
b- Justifie l’égalité : BÂH = 90° – HÂC
c- Que peut-on dire pour les angles BÂH et AĈH ?
d- Montre que tan AĈH = 3/4
e- En utilisant le triangle BAH, exprime tan (BÂH) en fonction de BH.
f- Déduis des questions précédentes que BH = 3,6 cm.
g- Cacule la mesure, arrondie au degré, de l’angle AĈH.
Exercice 9 (extrait de brevet)
Juliette mesure l’angle entre l’horizontale et le haut du réservoir d’un château d’eau grâce à un appareil placé à 1,70 m du sol. Elle trouve 58°.
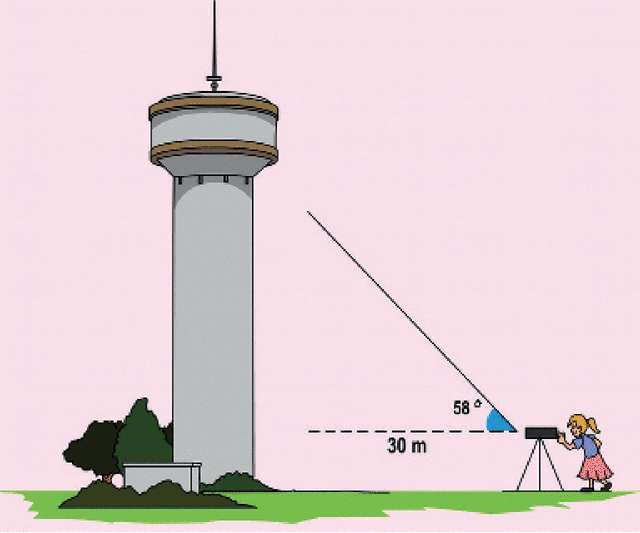
a- Cacule la hauteur du château d’eau arrondie au mètre.
b- La contenance de celui-ci est de 500 m³ d’eau. Calcule le diamètre de la base en considérant que le réservoir du château d’eau est cylindrique. Arrondis au décimètre.