I-Arithmétique
Arithmétique (Partie 3)
III-Décomposer un entier en produit de facteurs premiers
Propriété (admise)
Tout entier naturel supérieur ou égal à 2 peut s’écrire comme un produit de facteurs premiers.
Exemple
60 = 2x2x2x3x5
728 =2x2x2x7x13
Propriété
Pour un entier naturel donné, il n’existe qu’une seule décomposition en produit de facteurs premiers (sans tenir compte de l’ordre des facteurs).
Méthode pour décomposer un nombre en produit de facteurs premiers
Pour décomposer un nombre entier en produit de facteurs premiers :
-On écrit ce nombre comme un produit de deux facteurs.
-On recommence avec les facteurs qui ne sont pas premiers, jusqu’à n’avoir que des nombres premiers.
Sinon, on effectue des divisions successives par les nombres premiers diviseurs du nombre.
Exemple
Pour décomposer 300, on commence par le diviser par le plus petit nombre premier qui est 2 car 300 est pair, ensuite 3 …et on s’arrête quand on obtient 1.
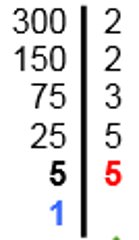
La décomposition de 300 est 300 = 2x2x3x5x5
Applications de la décomposition
a-Diviseurs d’un nombre entier
Comment trouver tous les diviseurs d’un nombre entier à partir de sa décomposition en produit de facteurs premiers ?
Trouver tous les diviseurs de 40.
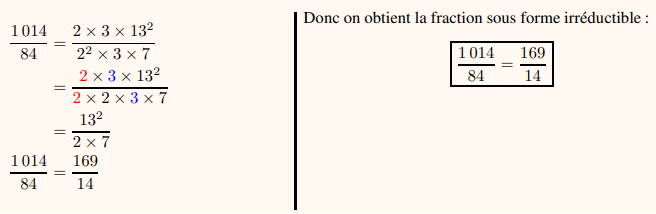
b-Fractions irréductibles
Une fraction est dite irréductible lorsque le numérateur et le dénominateur n’ont pas de diviseur commun autre que 1.
Exemple :
c-Calculer le Plus Grand Commun Diviseur de deux entiers
On écrit la décomposition des entiers en facteurs premiers.
On recherche les facteurs communs des deux entiers
On calcule alors le produit des facteurs communs.
Pour résumer, le PGCD de deux nombres entiers a et b supérieurs ou égaux à 2 a pour décomposition en facteurs premiers le produit des facteurs premiers apparaissant à la fois dans la décomposition de a et de b.
Exemple :
Calcul du Plus Grand Commun Diviseur de 126 et 180
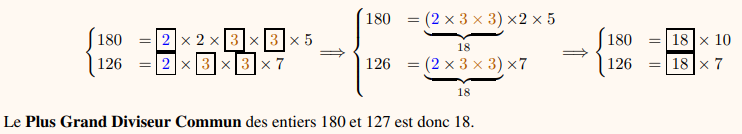
Exercice d’application numéro 1:
Un fleuriste possède un lot de 126 tulipes et 450 roses, il souhaite réaliser des bouquets ayant la même composition.
Combien peut-il en réaliser ?
Quel est le nombre maximal de bouquets qu’il peut réaliser ? Justifiez votre réponse.
Exercice d’application numéro 2 : multiples ou diviseurs ?
Deux voitures partent en même temps de la ligne de départ et font plusieurs tours d’un même circuit.
La voiture A fait le tour du circuit en 36 minutes et la voiture B en 30 minutes.
Y-a-t-il des moments (autres que le départ !) où les voitures se croisent sur la ligne de départ ?