I-Arithmétique

I. Vocabulaire et définitions

a) Qu’est-ce qu’une division euclidienne ?

Euclide 300 avant J-C Source (https://fr.wikipedia.org/wiki/Euclide)

Définition : Effectuer la division euclidienne de a par b, c’est trouver le quotient q et le reste r tels que :

a = b x q + r et 0 ≤ r < b

Effectuer la division euclidienne de 349 par 6 signifie :

Dans 349 combien y-a-t-il de 6 ?

Dans 349, il y a 49 fois 7 et il reste 6 Soit 349 = 49×7 + 6

Avec la calculatrice, on peut effectuer la division euclidienne de 349 par 7

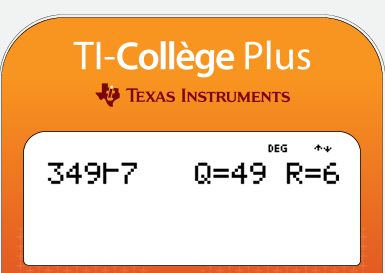
Exercice d’application

Effectue la division euclidienne de 183 par 12.
278 = 6 × 45 + 8 : quelle(s) division(s) euclidienne(s) cette égalité
représente-t-elle ?

Exemples :

On partage 96 bonbons entre 20 élèves.

Combien chaque élève aura-t-il de bonbons ?

Réponse : Chaque élève reçoit 4 bonbons et il reste : 16 bonbons.

Avec 96 bonbons, combien de sachets de 20 bonbons peut-on faire ?

Réponse : On peut faire 4 sachets de 20 bonbons et il reste : 16 bonbons.

On partage 96 € entre 20 élèves.

Quelle somme chaque élève va-t-il toucher ?

Réponse : Chaque élève recevra : 4,80 €.

b) Division euclidienne :

Lorsque dividende, diviseur, quotient et reste sont entiers, on parle de division euclidienne.

Effectuer la division euclidienne de 25 par 3, c’est déterminer le quotient q et le reste r tel que : 25 = 3 x q + r avec r < 3

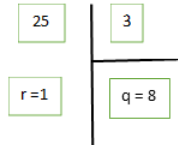
Effectuer la division euclidienne de a par b, c’est déterminer le quotient q et le reste r tel que : a = b x q + r avec r < b

c) Critères de divisibilité :

Un nombre entier est divisible par 2, s’il se termine par 0 ; 2 ; 4 ; 6 ou 8 (c’est un nombre pair).

• Un nombre entier est divisible par 5, s’il se termine par 0 ou 5.

• Un nombre entier est divisible par 3, si la somme de ses chiffres est un multiple de 3.

• Un nombre entier est divisible par 9, si la somme de ses chiffres est un multiple de 9.

• Un nombre entier est divisible par 4, si ses deux derniers chiffres forment un multiple de 4.

Exemple :

1-Le nombre 2781 est-il divisible par 2, par 3 et par 9 ?

2-Donne tous les diviseurs de 40.

Pour imprimer la leçon Télécharger

Exercice d’application

Effectue la division euclidienne de 183 par 12.
278 = 6 × 45 + 8 : quelle(s) division(s) euclidienne(s) cette égalité
représente-t-elle ?

Correction

On peut donc écrire :

183 = 12 × 15 + 3 avec 3 < 12.

8 < 45 mais 8 > 6 donc l’égalité représente la division euclidienne de 278 par 45 mais ne peut pas représenter celle de 278 par 6

d) Comment savoir si un nombre est diviseur d’un autre nombre ?

Définition : Un nombre a est divisible par un nombre b lorsque le reste de la division euclidienne de a par b est nul, c’est à dire lorsque le quotient de a par b est un nombre entier.
On dit alors que b est un diviseur de a et que a est un multiple de b
Remarques :
● 1 est un diviseur de tout entier
● Chaque entier est divisible par lui-même.
Exemple :
● 18 est divisible par 6 car 18 = 6 × 3 + 0
On dit que 6 et 3 sont des diviseurs de 18 et que 18 est un multiple de 6 et de 3.

e) Comment trouver tous les diviseurs d’un entier naturel ?

Propriété : Pour trouver tous les diviseurs d’un nombre entier 𝑛, on teste la divisibilité de 𝑛 par tous les nombres entiers inférieurs ou égaux à √𝑛.

Exemple : Pour trouver tous les diviseurs de 100, on teste la divisibilité avec tous les entiers inférieurs ou égaux à 10.

Méthode commentée en vidéo

Activité : « Le nombre caché »

Je suis un nombre entier compris entre 100 et 400.

Je suis pair.

Je suis divisible par 11.

J’ai aussi 3 et 5 comme diviseurs.

Qui suis-je ?”.

Expliquer une démarche permettant de trouver le nombre caché,

et donner sa valeur.

Activité : « LE PROBLÈME DU CENTURION »

Le centurion ordonne à ses légionnaires : « Rangez-vous par 4 ! ». Les soldats s’exécutent, mais le dernier rang est incomplet : il ne compte que 3 soldats.

« Mettez-vous par 5 ! », hurle alors le centurion ; mais au dernier rang,
incomplet, on compte de nouveau 3 soldats.

« Eh bien, rangez-vous par 7 ! ». Encore une fois, le dernier rang reste
incomplet : on y compte toujours 3 soldats.